Тема 15. Игры в условиях неопределенности. Критерий принятия решений

Пусть в игре с природой П игрок А обладает т возможными чистыми стратегиями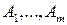, а природа П может находиться в одном из п состояний 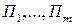. Пусть (22.1) является матрицей выигрышей игрока А.

Обобщенный критерий пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами.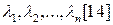

Переставим выигрыши 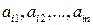при каждой стратегии 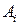(т. е. элементы каждой строки матрицы (22.1)), расположив их в неубывающем порядке, и обозначим элементы полученной матрицы через 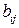, а саму матрицу - через В:

B =				…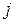
			…
			…
…	…	…	…	…
			…

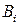
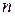
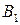
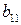
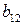
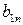
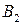
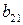
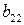
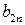
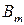
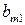
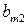
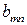
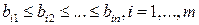. (15.1)

Каждая строка 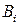матрицы В является перестановкой выигрышей при стратегии 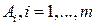. Не исключена возможность, что для некоторых номеров 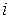и 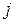будет иметь место равенство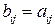. В силу неравенств (23.1) в первом столбце матрицы В стоят минимальные выигрыши при каждой стратегии

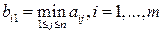, (15.2)

а в последнем 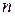-м столбце - максимальные выигрыши при каждой стратегии

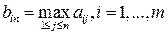. (15.3)

Пусть числа 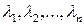удовлетворяют условиям

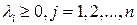и 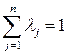. (15.4)

Показателем эффективности стратегии 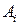по рассматриваемому критерию назовем число

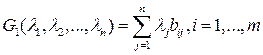. (15.5)

Из этого определения видно, что показатель эффективности стратегии 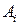учитывает все выигрыши при этой стратегии 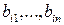и зависит от чисел 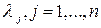, удовлетворяющих условиям (15.4).

Обобщенным критерием пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами 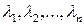, назовем критерий, по которому оптимальной среди чистых стратегий считается стратегия 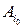с максимальным показателем эффективности (15.5), т.е.

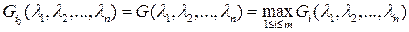
Числа

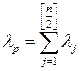и 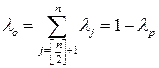(15.6)

назовем показателями соответственно пессимизма и оптимизма. В обозначениях (15.6) индекс 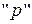- первая буква английского pessimism, индекс "о" - первая буква английского optimism, а 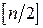- целая часть числа 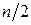, т. е. наибольшее целое число, не превосходящее числа 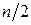; очевидно, что

Коэффициенты 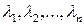выбираются из субъективных соображений следующим образом: чем опаснее ситуация, тем больше возтникает желание в ней подстраховаться, тем больше, т. е. ближе к единице, должен быть коэффициент пессимизма 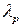(см. (15.6)) и, следовательно, тем меньше, т.е. ближе к нулю, будет коэффициент оптимизма 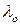. В безопасной ситуации коэффициенты 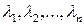выбираются так, чтобы показатель пессимизма 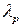был ближе к нулю, а показатель оптимизма 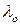- ближе к единице. Таким образом, показатели пессимизма 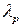и оптимизма 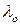в данном критерии выражают количественную меру соответственно пессимизма и оптимизма игрока А, выбирающего коэффициенты .

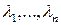Если показатель оптимизма 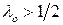и, следовательно, показатель пессимизма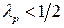, то критерий - более "оптимистический", чем "пессимистический"; если, наоборот, показатель оптимизма 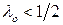и, следовательно, показатель пессимизма , то критерий - более "пессимистический", чем "оптимистический"; если же показатели оптимизма и пессимизма равны: 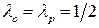, то критерий можно считать реалистическим.

Критерий Вальда (критерий крайнего пессимизма). Критерий Вальда есть частный случай обобщенного критерия Гурвица относительно выигрышей со специальными коэффициентами

. (15.7)

которые, очевидно, удовлетворяют условиям (14.4).

Подставляя значения коэффициентов (15.7) в формулу (15.5) и учитывая (15.2), получим показатель эффективности стратегии 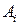по критерию Вальда:

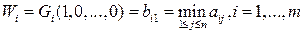. (15.8)

представляющий собой минимальный выигрыш игрока А при применении им стратегии 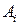. Оптимальной среди чистых стратегий по критерию Вальда является, таким образом, стратегия 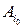, имеющая максимальный показатель эффективности (15.8):

.

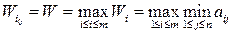Максимаксный критерий (критерий крайнего оптимизма). Противоположностью критерию Вальда является так называемый максимаксный критерий, представляющий собой также частный случай обобщенного критерия Гурвица относительно выигрышей, когда коэффициенты 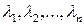выбираются следующим образом:

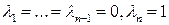. (15.9)

Тогда оптимальной среди чистых стратегий по максимаксному критерию является стратегия 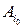с максимальным показателем эффективности

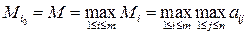, (15.10)

т.е. стратегия, максимальный выигрыш при которой максимален среди максимальных выигрышей всех чистых стратегий. По-другому можно сказать, что оптимальной будет та чистая стратегия, при которой (хотя бы) один из выигрышей является максимальным среди выигрышей всех чистых стратегий. Оптимальная по максимаксному критерию стратегия гарантирует игроку А возможность наибольшего выигрыша, равного максимаксу

.

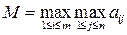Критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем оптимизма 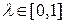. Данный критерий является как бы промежуточным между критериями крайнего пессимизма и крайнего оптимизма и представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей с коэффициентами

,

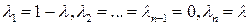удовлетворяющими, очевидно, условиям (15.4).

Оптимальной же стратегией по этому критерию считается стратегия 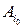с максимальным показателем эффективности

.

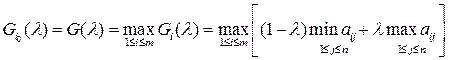Дата добавления: 2014-01-06