Понятие позиционной игры и ее нормальной формы

Тема 16. Позиционные игры

Естественным расширением матричной игры двух игроков с нулевой суммой является позиционная игра, в которой может принимать участие более двух (конечное число) игроков, каждый из них может последовательно делать конечное число ходов, некоторые ходы могут быть случайными, а сведения о них могут меняться от хода к ходу. Такие игры могут быть формализованы, определенным образам преобразованы в игру, эквивалентную некоторой матричной игре двух игроков с нулевой суммой. Процесс сведения позиционной игры к матричной называется нормализацией, а полученная матричная игра — игрой в нормальной форме.

Рассмотрим сначала пример, иллюстрирующий этот процесс.

Пример. Игра состоит из трех ходов, которые делают два игрока. Первый ход делает первый игрок: он выбирает число 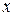из множества двух чисел .

Второй ход делает второй игрок: зная, какое число 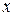выбрано первым игроком в первом ходе, он выбирает число у из множества двух чисел .

Третий ход делает первый игрок: зная, какое число у выбрал второй игрок, и помня, какое число 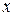он выбрал при первом ходе, выбирает число 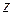из множества двух чисел . На этом игра заканчивается и происходит распределение выигрышей, второй игрок платит первому сумму, определенную функцией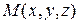, где М задана следующим образом:

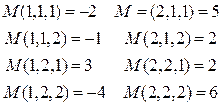
Для сведения этой позиционной игры к нормальной форме воспользуемся понятием стратегии игрока, как набора правил и указаний, как надо поступать ему во всех мыслимых ситуациях или при любом мыслимом состоянии информации, получаемой в любой момент игры. Рассмотрим сначала мыслимые стратегии второго игрока. Ясно, что у него имеется возможность выбора одного из двух чисел 1 или 2, т. е. имеется две возможности. Кроме того, у него есть информация о выбранном числе при первом ходе, следовательно, он, выбирая число у, может учитывать или не учитывать эту информацию, поэтому для каждого у имеется еще два значения , т. е. всего четыре стратегии:

1-я – выбирать y=1, не взирая на ,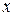

2-я – выбирать y=2, не взирая на ,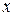

3-я – выбирать y=,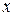

4-я – выбирать y=1, если 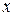=2, и выбирать y=2, если 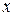=1.

Другими словами, у второго игрока столько стратегий, сколько имеется способов отображения множества в себя.

Стратегия для первого игрока должна учитывать результаты сделанных ранее выборов. При каждом выборе на первом ходе может быть два выбора на втором ходе, т. е. уже имеется четыре варианта, а при каждом из этих вариантов может быть сделано два выбора, т. е. всего 8 возможных стратегий. Обозначим через 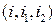стратегию первого игрока: где 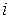означает выбор первым игроком на первом ходе; 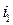— выбор первым игроком на третьем ходе, если второй игрок на втором ходе выбрал число 1: 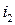— выбор первым игроком на третьем ходе, если второй на втором ходе выбрал число 2.

Например, 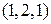означает следующую стратегию первого игрока: на первом ходе он выбирает число 1 (первая цифра в скобках), а на третьем ходе он выбирает число 2, стоящее на втором месте в скобках, если второй игрок на втором ходе выбрал число 1; если же второй игрок на втором ходе выбрал число 2, то первый игрок на третьем ходе должен выбрать число 1, стоящее на третьем месте в скобках.

Теперь приведем матрицу выигрышей первого игрока в зависимости от применяемых стратегий (табл. 1), где столбцы соответствуют стратегиям второго игрока, а строки — стратегиям первого игрока.

Таблица 1

1,1,1 1,1,2 1,2,1 1,2,2 2,1,1 2,1,2 2,2,1 2,2,2	1,1,1=-2 1,1,1=-2 1,1,2=-1 1,1,2=-1 2,1,1=5 2,1,1=5 2,1,2=2 2,1,2=2	1,2,1=3 1,2,2=-4 1,2,1=3 1,2,1=-4 2,2,1=2 2,2,2=6 2,2,1=2 2,2,2=6	1,1,1=-2 1,1,1=-2 1,1,2=-1 1,1,2=-1 2,2,1=2 2,2,2=6 2,2,1=2 2,2,2=6	1,2,1=3 1,2,2=-4 1,2,1=3 1,2,2=-4 2,1,1=5 2,1,1=5 2,1,2=2 2,1,2=2

Дата добавления: 2014-01-06