Термодинамические условия равновесия химических реакций

Ранее было показано, что общим условием равновесия термодинамической системы является максимальное значение ее энтропии, математическим выражением которого являются соотношения

ds = 0 и d²s < 0.

В некоторых случаях, в частности для химических реакций, это условие может быть выражено и через другие функции состояния системы.

Так, объединенное аналитическое выражение первого и второго законов термодинамики для системы, в которой не совершается полезная работа,

TdS ≥ dU + pdV

или

dU -TdS + pdV ≤ 0

для изохорно-изотермических реакций, протекающих без совершения полезной работы, при V = const и T = const принимает вид:

dU - TdS ≤ 0

или в конечной форме

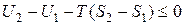. (14.18)

Этому выражению можно придать другой вид

.

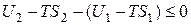Величина U –TS, являющаяся функцией состояния, поскольку все входящие в нее величины зависят только от состояния системы, называется свободной энергией и обозначается буквой F. Смысл этого названия будет виден из дальнейшего.

Таким образом,

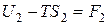и ,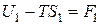

следовательно, для изохорно – изотермических систем получаем

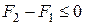, (14.19)

где знак равенства относится к обратимым, а знак неравенства – к необратимым изменениям системы.

Полученное соотношение показывает, что при обратимых изменениях изохорно-изотермических систем их свободная энергия остается без изменения, а при необратимых – уменьшается.

Это означает, что равновесие таких систем, создающееся в результате термодинамически необратимых изменений в них, наступает при достижении их свободной энергией минимума, когда

dF = 0 и d²F > 0. (14.20)

Полученные соотношения и выражают аналитическое равновесие изохорно– изотермических систем.

Аналогично этому общее уравнение

dU – TdS + pdV ≤ 0

для изобарно – изотермических реакций, протекающих при p = const и

Т = const, в конечной форме примет вид

, (14.21)

или

,

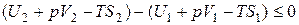или, наконец,

, (14.22)

где I – энтальпия системы.

Функция состояния I – TS называется изобарным потенциалом и обозначается через Z. Таким образом,

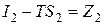и ,

следовательно, для изобарно – изотермических систем получаем

Z2 – Z1 ≤ 0, (14.23)

т. е. при обратимых изменениях изобарно-изотермических систем их изобарный потенциал остается без изменения, а при необратимых изменениях – уменьшается.

Это означает, что равновесие изобарно-изотермических систем, создающееся в результате необратимых изменений в ней, наступает при минимальном значении изобарного потенциала и аналитически условие этого равновесия выражается соотношениями

dZ = 0 и d²Z > 0. (14.24)

Дата добавления: 2014-01-06