Уравнение изотермы химической реакции

Чем больше химическое сродство реагирующих веществ, тем больше максимальная работа реакции и тем больше полнота ее протекания, определяемая величиной константы равновесия. С увеличением полноты протекания реакции величина константы равновесия уменьшается, следовательно, между ней и максимальной работой реакции должна существовать некоторая обратная зависимость.

Для установления этой зависимости рассмотрим изотермическую реакцию, описываемую уравнением

aA+bB+... 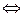cC+dD+...,.

условия протекания которой обеспечивают получение максимальной полезной работы.

Чтобы обеспечить эти условия, реакция должна осуществляться термодинамически обратимо, т. е. в каждый данный момент вся система в целом должна находиться в равновесном состоянии и только может переходить из одного равновесного состояния к другому, бесконечно близкому равновесному состоянию.

Осуществить практически такой процесс невозможно, но мысленно можно себе представить его происходящим в установке, схема которой, изображенная на рисунке 14.3, в несколько ином виде была предложена еще в XIX веке Вант-Гоффом.

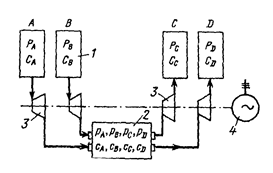
Установка состоит из емкостей 1, каждая из которых содержит в чистом виде соответствующий компонент реакции при постоянных давления Р и концентрации С, и сосуда 2, в котором находится равновесная смесь этих компонентов. Сосуд 2, называемый ящиком Вант-Гоффа, снабжен полупроницаемыми перегородками, пропускающими свободно лишь один из компонентов и совершенно не пропускающими всех остальных компонентов.

Емкости, содержащие исходные вещества.(давления которых Р больше равновесных давлений р), и емкости, содержащие конечные продукты (давления которых меньше равновесных давлений), сообщаются с ящиком Вант-Гоффа через турбины 3.

Исходные вещества проходят в эквивалентных количествах через турбины, в которых расширяются изотермически до равновесных давлений, а затем через полупроницаемые перегородки поступают в ящик Вант-Гоффа. Одновременно с этим из ящика Вант-Гоффа в эквивалентных же количествах отводятся через полупроницаемые перегородки продукты реакции. Последние также проходят через турбины, в которых изотермически расширяются до необходимого давления, после чего поступают в соответствующие емкости.

Техническая работа турбин используется в генераторе 4. Очевидно, что работа, передаваемая генератору, и представляет собой максимальную работу рассматриваемой реакции, т. е.

A = L_A + L_B+… +L_С + L_D+ ….

Учитывая, что техническая работа потока, отнесенная к n киломолям, при изотермическом процессе в аппарате выражается формулой

,

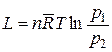в рассматриваемом случае получаем

,

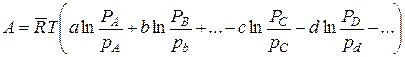откуда

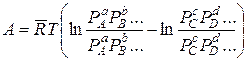
или

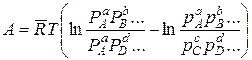
и окончательно

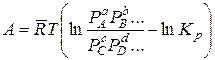. (14.39)

Полученное уравнение связывает максимальную работу реакции с константой равновесия и начальными давлениями веществ, участвующих в реакции, и называется уравнением изотермы данной реакции.

Воспользовавшись соотношениями (14.15) и (14.16), нетрудно получить уравнение изотермы реакции, выраженное не через парциальные давления и константу равновесия К_р, а через концентрации реагентов и константу равновесия К_С

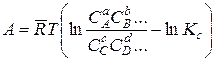. (14.40)

Следует заметить, что уравнения (14.39) и (14.40) в равной степени справедливы как для изохорно-изотермических, так и для изобарно-изотермических реакций. Однако при одинаковых исходных состояниях химической системы давления ее в соответствующих равновесных состояниях будут разными (если реакции идут с изменением количества киломолей). Поэтому и подставляемые в эти уравнения величины констант равновесия К_С или К_р будут разными, а поскольку исходные парциальные давления (или концентрации) в обоих случаях одинаковы, подсчитываемые по этим уравнениям значения A_V и А_P будут тоже разными (также при условии, что Δ n ≠ 0). Практически применительно к изохорно-изо-термическим реакциям удобнее пользоваться уравнением (14.40), а применительно к изобарно-изотермическим реакциям – уравнением (14.39).

Ранее было показано, что ес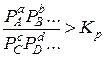ли

или ,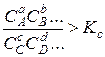

то химическая система находится в неравновесном состоянии и скорость у прямой реакции больше, чем у обратной, т. е. результирующая реакция протекает в сторону образования конечных продуктов из исходных веществ. Отсюда следует, что если максимальная работа, вычисленная по уравнению изотермы реакции, положительна, то при заданных начальных условиях возможна лишь прямая реакция. Наоборот, если максимальная работа получается отрицательно, и, то возможна лишь обратная реакция. Наконец, если максимальная работа равна нулю, то система находится в равновесии и видимого течения реакции нет вообще.

Уравнение изотермы реакции показывает, что максимальная работа одной и той же реакции при одной и той же температуре может быть различной, поскольку она зависит от начальных значений концентраций (или парциальных давлений) компонентов реакции. Поэтому для сравнительной оценки химического сродства различных реакций исходные концентрации компонентов принимаются равными единице. Тогда первое слагаемое уравнения изотермы реакции обращается в нуль и химическое сродство, измеряемое величиной максимальной работы, может быть вычислено по формулам

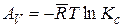и 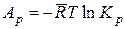. (14.41)

Эти значения химического сродства различных реакций при разных температурах приводятся обычно в таблицах.

14.14 Закон Вант – Гоффа

Как показывает опыт, положение химического равновесия обратимых реакций зависит от температуры, следовательно, от нее зависят и константы равновесия К_С и К_Р.

Чтобы установить эту зависимость для изохорно-изотермических реакций, продифференцируем по Т при V = const уравнение (14.40).

Считая, что начальные концентрации компонентов реакции заданы и, следовательно, в этом уравнении первый член в скобках является величиной постоянной, получаем

.

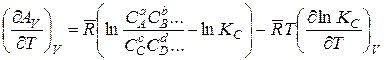Подставляя полученную производную в уравнение Гиббса –Гельмгольца (14.38), получаем

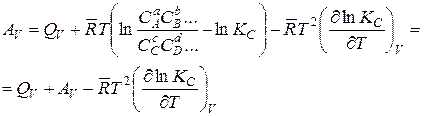
или

. (14.42)

Аналогично этому для изобарно – изотермических реакций из уравнения (14.39) получаем

.

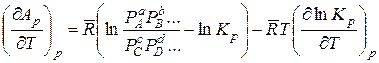Подставляя полученную частную производную в уравнение (14.38), находим

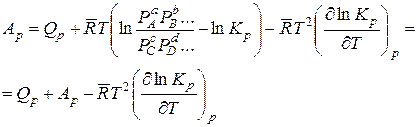
или

. (14.43)

Объединяя выведенные формулы, получаем уравнение, устанавливающее в дифференциальной форме зависимость константы равновесия изохорно-изотермических реакций от температуры, при которой они протекают

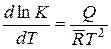. (14.44)

Эта зависимость носит название закона Вант-Гоффа. Иногда ее в виде, написанном для изохорно-изотермической или изобарно-изотермической реакции, называют соответственно изохорой или изобарой изотермической реакции.

Непосредственно из закона Вант-Гоффа следует, что если Q > 0, то и dlnK/dT > 0, т.е. экзотермических реакциях с увеличением температуры константа равновесия увеличивается (так как если производная функция положительна, то с увеличением аргумента возрастает и сама функция). Значит, с увеличением температуры равновесие сдвигается влево и выход продуктов реакции уменьшается. Наоборот, если Q < 0, то и dlnK/dT <0, т. е. в эндотермических реакциях с увеличением температуры константа равновесия уменьшается, т. е. равновесие сдвигается вправо и выход продуктов реакции увеличивается.

Если известно значение константы равновесия К₁ рассматриваемой реакции при какой-либо температуре T₁, то, интегрируя уравнение, выражающее закон Вант-Гоффа, можно получить значение константы равновесия К₂ этой же реакции при любой другой температуре Т₂.

Действительно, этому уравнению можно придать вид

,

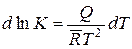а после интегрирования

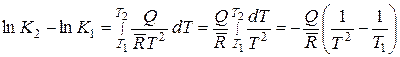
или

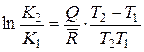. (14.45)

В этой формуле Q – среднее значение теплового эффекта реакции в заданном интервале температур. Оно не учитывает действительную зависимость теплового эффекта от температуры, а потому является приближенным, причем точность его с уменьшением интервала температур повышается. Эта же формула позволяет определить средний тепловой эффект реакции в заданном интервале температур, если известны значения констант равновесия при крайних температурах этого интервала. Для этого случая формула принимает вид

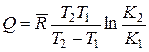. (14.46)

В качестве примера определим тепловой эффект реакции

NО ↔ 0,5 N₂+0,5 О₂, если известно, что при T₁=1811°K константа равновесия K₁=9,16·.10^-3, а при Т₂ = 2195⁰K константа равновесия К₂=24,2.·10^-3.

Приняв, что практически тепловой эффект от температуры не зависит, получим

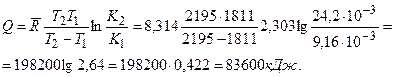
Однако имеются реакции, для которых экспериментальное определение констант равновесия или очень сложно, или совсем неосуществимо. В таких случаях выражение (14.44) приводит к неопределенному интегралу

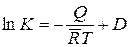, (14.47)

где D – константа интегрирования. Вычисление ее, которое стало возможным лишь после установления излагаемого ниже теплового закона Нернста, здесь не рассматривается.

Дата добавления: 2014-01-06