Технология решения физических задач

Под технологией решения задачи понимают совокупность приемов и операций, выполнение которых приводит к ответу на вопрос задачи, к нахождению связи между искомым и заданным в ее условии.

В психологии процесс мышления чаще всего определяется как аналитическо-синтетический. Логические приемы, осуществляемые при решении задач, также в себя включают анализ и синтез, которые сопровождают друг друга. В то же время аналитический и синтетический приемы часто рассматривают раздельно хотя это деление является условным.

При использовании аналитического приема решение задачи начинают с анализа вопроса задачи и записи формулы, в которую входит искомая величина. Затем для величин, содержащихся в этой формуле, записывают уравнение, устанавливающее их связь с величинами, заданными в условии.

При использовании синтетического приема решение задачи начинают с выяснения связей величин, данных в условии задачи, с другими до тех пор, пока в уравнение в качестве неизвестной не войдет искомая величина.

Деятельность учителя при решении задач заключается в обучении учащихся решению физических задач, что представляет собой систему приемов (или технологию), реализация которых приводит формированию у учащихся умений решать задачи.

Решение любой задачи включает в себя несколько этапов. При обучении учащихся необходимо прежде всего сформировать у них представления об этих этапах и необходимости следовать им при решении задачи.

Первый этап решения задачи - чтение и уяснение условия.

Условие задачи читает либо сам ученик, либо учитель. Текст задачи читается без спешки, при необходимости повторяется, учащимся разъясняются незнакомые термины и понятия. Полезно проанализировать условие, определив, какое явление описано в задаче что дано, что надо найти. На первых этапах обучения решению задач полезно просить учащихся пересказать условие задачи.

Второй этап решения задачи - краткая запись условия задачи. Условие записывают столбиком, при необходимости оставляют место для записи табличных данных, потребность в которых ус­танавливается при анализе задачной ситуации.

Третий этап решения задачи - перевод заданных значений физических величин в Международную систему единиц (СИ). К неукоснительному выполнению этого этапа следует приучать учащихся с начальных классов, что обусловлено в том числе и затруднения­ми, испытываемыми учащимися при выполнении этой работы. В дальнейшем допустимо использование внесистемных единиц, разрешенных к употреблению.

Четвертый этап решения задачи - анализ описанной в ней заданной ситуации. Итогом выполнения этого этапа является модель задачной ситуации.

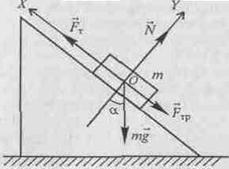
В ходе анализа устанавливают, какой физический объект описывается в задаче, какие происходят изменения состояния объекта, что является их причиной. Анализ задачной ситуации сопровождают рисунком, схемой, чертежом. В задачах по механике выбирают систему отсчета, анализируют взаимодействия, изображают силы.

Важным при анализе задачной ситуации является обсуждение всех допущений, которые делают при ее решении (факторов, которыми можно пренебречь), например пренебрежение размерами тела (материальная точка), массой нити, связывающей движущиеся тела (одинаковость ускорений тел), теплообменом с окружающей средой (изолированная система) и т.п.

Пятый этап решения задачи - создание математической модели решения задачи (составление плана решения, запись уравнении, решение задачи в общем виде, т.е. получение выражения, связы­вающего искомую величину с данными).

Шестой этап решения задачи - вычисления. Перед выполнением вычислений целесообразно осуществить проверку полученного выражения по единицам величин. Такая проверка позволяет подставить в расчетную формулу лишь численные значения величин без соответствующих единиц. Если проверка не осуществляется, то учащиеся должны подставлять в формулу значения величин (численные значения с соответствующими единицами).

С едьмой этап решения задачи - проверка ответа и его анализ. При анализе ответа устанавливают его реальность и его измене­ние при учете тех факторов, которыми пренебрегали при составлении физической модели задачной ситуации.

Этапы решения задачи представляют собой определенную последовательность действий и в этом смысле могут рассматриваться как алгоритм. Этот алгоритм является общим и содержит последовательность действий, не зависящую от того, к какому разделу курса физики относится задача. Возможно - составление частных алгоритмов решения задач или последовательности действии при решении задач по тому или иному разделу курса физики по той или иной теме.

Алгоритм, который используется в обучении, отличается от математического алгоритма меньшей жесткостью. Поэтому его называют алгоритмическим предписанием или предписанием алго­ритмического типа.

Алгоритмическое предписание - точное, общепринятое выполнение в определенной последовательности элементарных операций для ре­шения любой из задач, принадлежащих к некоторому классу или типу.

В качестве примера приведем алгоритм решения задач на газо­вые законы.

1. Чтение и разъяснение условия задачи.

2. Краткая запись условия задачи.

3. Перевод значений величин в СИ.

4. Анализ задачной ситуации:

- выделить объект (газ), состояние которого исследуется;

- сделать рисунок, отметив параметры, характеризующие каждое состояние газа;

- установить, какие параметры газа изменяются;

- переформулировать условие задачи на языке физической модели.

5. Создание математической модели задачи:

-записать уравнение Клапейрона, если неменяются масса и состав газа;

-записать формулу одного из газовых законов, если не меняются масса и состав газа и один из параметров его состояния;

-записать уравнение Менделеева-Клапейрона, если меняются масса и состав газа, а также параметры его состояния;

- записать дополнительные уравнения;

- выразить искомую величину.

6. Выполнение вычисления.

7. Проверка и анализ ответа.

Работа по формированию у учащихся алгоритмического приема решения задач может быть построена по-разному в зависимости от уровня подготовки учащихся.

В классе с сильным составом учащиеся сами составляют и записывают алгоритмическое предписание, решив задачи самостоятельно или с помощью учителя. В классе, учащиеся которого не обладают высокими физико-математическими способностями, учитель дает алгоритмическое предписание в готовом виде и показывает его применение к решению задачи. В классе со слабым составом учащихся предписание дается в готовом виде и отрабатывается каждое его действие.

Полезно на первых этапах обучения учащихся решению задач определенного класса повесить плакат с последовательностью действий или выписать их на доске.

Применение алгоритмических предписаний имеет определенные границы. В частности, такие детализированные предписания при обучении учащихся решению творческих задач невозможны и нецелесообразны, хотя общие этапы деятельности могут быть определены и в этом случае.

При анализе задачной ситуации может быть использован метод графов. Он позволяет лучше уяснить аналитико-синтетический прием решения задачи, наглядно представить процесс анализа задачи, последовательность действий при ее решении.

Г раф - это совокупность множества точек (вершин) и множества прямых (ребер), соединяющих эти точки. Ориентированный граф - такой, ребра которого имеют определенное направление.

Рассмотрим применение метода графов на примере следующей задачи.

Задача. Сила тока в спирали нагревателя 0,6 А. Сопротивление спирали 60 Ом. Определите изменение температуры воды массой 6 кг, если нагреватель работал 7 мин.

При анализе задачи выясняют, что вода нагревается за счет энергии, выделяющейся при прохождении по спирали электри­ческого тока. При этом считают, что все выделяющееся количе­ство теплоты пошло на нагревание воды, и пренебрегают поте­рями на нагревание сосуда, в который налита вода, окружающего воздуха и др.

Рассуждения ведутся в следующей логической последователь­ности: чтобы найти разность температур Дг, нужно знать количе­ство теплоты (0п), полученное водой, ее массу (т) и удельную те­плоемкость (с). Чтобы найти количество теплоты (бот), отданное спиралью при прохождении по ней электрического тока, нужно знать сопротивление спирали, силу тока и время ее работы т.

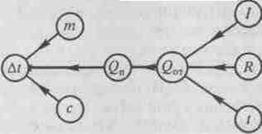Рис. 1

По ходу рассуждений выстраивают граф (рис.1), вершинам которого являются физические величины, а ребрами - связи между ними. После построения графа ребрам приписывают направления соответствующего поиска решения задачи.

Затем записывают уравнения, число которых равно числу вершин графа, в которые входят или из которых выходят не менее двух ребер. В данной задаче таких вершин три, следовательно, уравнений - три:

Q_от = I²Rτ; Q_от = Q_п; Q_п = const

Окончательно: Δt = I²Rτ / cm

Физические задачи решают на всех основных видах занятий - на уроках физики, на внеклассных занятиях, на внешкольных мероприятиях.

Задачи занимают разное место на уроке в зависимости от той дидактической цели, которую преследует их решение. Тренировочные вычислительные и простые качественные задачи решают после объяснения нового материала для его иллюстрации и закрепления.

Задачи решают в начале урока при повторении учебного материала или проведении проверки усвоения материала, в конце урока при закреплении изученного материала. Перед объяснением нового материала задачи решают и для актуализации знаний учащихся, и для создания проблемной ситуации.

Для обучения учащихся решению задач проводят, как правило, специальные уроки, которые находят отражение в календарном плане учителя.

Процесс обучения учащихся решению задач планируется так же, как и любая деятельность учителя. При этом формирование умения решать задачи следует начинать с простых задач, постепенно шаг за шагом усложняя их. В противном случае учащимся приходится прикладывать большие усилия для преодоления возникающих трудностей. Подбирая задачи по возрастанию степени сложности, учитель выстраивает определенную систему. Примером такой системы может служить система задач по динамике, приведенная ниже:

- задачи на движение одного тела при действии силы тяжести;

- задачи на движение одного тела при действии силы упругости;

- задачи на движение одного тела при действии силы трения;

-задачи на движение одного тела в вертикальном направле­нии, в горизонтальном направлении, на наклонной плоскости при действии двух сил;

- задачи на движение одного тела при действии трех сил;

- задачи на движение связанных тел: в вертикальном направлении; в горизонтальном направлении; одного - в горизонталь­ном направлении, другого - в вертикальном; одного - в вертикальном направлении, другого - на наклонной плоскости.

Физические задачи широко применяются при проверке знаний и умений учащихся. Чаще всего это осуществляется в виде контрольных работ.

Много задач учащиеся решают самостоятельно в виде домашних заданий. Учитель практически каждое теоретическое домашнее задание комбинирует с физическими задачами по изучаемому материалу. В ряде случаев целесообразно давать учащимся рекомендации по решению задач, которые предложены в качестве домашнего задания. Сложные задачи, оказавшиеся трудными для учащихся при решении их дома, надо решить в классе на следующем уроке. Можно предложить показать решение задачи ученика, сумевшего решить ее, либо решить самому учителю на доске с со­ответствующими пояснениями.

Задачи решают и на внеклассных занятиях. Это может быть кружок по решению задач для учащихся, интересующихся физи­кой, занятия с учащимися по подготовке к экзамену по физике (если он запланирован) или при подготовке желающих учеников к конкурсным (вступительным) экзаменам в вузы. В этих случаях решают в основном сложные задачи. Задачи решаются и на факультативных занятиях по физике.

ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ

Дата добавления: 2014-01-06