
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределения Максвелла и Больцмана
|
|
|
|
Распределение Максвелла (распределение молекул газа по скоростям). В равновесном состоянии параметры газа (давление, объем и температура) остаются неизменными, однако микросостояния — взаимное расположение молекул, их скорости — непрерывно изменяются. Из-за огромного количества молекул практически нельзя определить значения их скоростей в какой-либо момент, но возможно, считая скорость молекул непрерывной случайной величиной, указать распределение молекул по скоростям.
Выделим отдельную молекулу. Хаотичность движения позволяет, например, для проекции скорости ux молекулы принять нормальный закон распределения. В этом случае, как показал Дж. К. Максвелл, плотность вероятности записывается следующим образом:
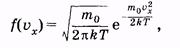 |
(2.28)
где т0 — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.
Аналогичные выражения могут быть получены для f(uу) и f(uz).
На основании формулы (2.15) можно записать вероятность того, что молекула имеет проекцию скорости, лежащую в интервале от ux до ux + duх:
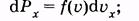
(2.29)
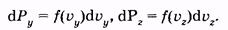 (2.30) (2.30)
|
аналогично для других осей
 (2.31) (2.31)
|
Каждое из условий (2.29) и (2.30) отражает независимое событие. Поэтому вероятность того, что молекула имеет скорость, проекции которой одновременно удовлетворяют всем условиям, можно найти по теореме умножения вероятностей [см. (2.6)]:
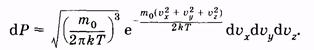 (2.32) (2.32)
|
Используя (2.28), из (2.31) получаем:
Отметим, что из (2.32) можно получить максвелловскую функцию распределения вероятностей абсолютных значений скорости (распределение Максвелла по скоростям):
 (2.33) (2.33)
|
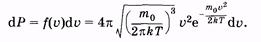 (2.34) (2.34)
|
и вероятность того, что скорость молекулы имеет значение, лежащее в интервале от u до u + du:
|
|
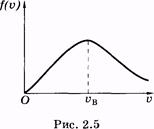
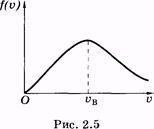
График функции (2.33) изображен на рисунке 2.5. Скорость, соответствующую максимуму кривой Максвелла, называют наивероятнейшей u в. Ее можно определить, используя условие максимума функции:
 или
или 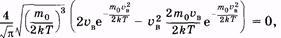
откуда

|
(2.35)
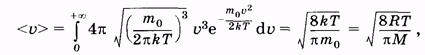 (2.36) (2.36)
|
Среднюю скорость молекулы (математическое ожидание) можно найти по общему правилу [см. (2.20)]. Так как определяется среднее значение скорости, то пределы интегрирования берут от 0 до ¥ (математические подробности опущены):
где М = т0 N A — молярная масса газа, R = k N A — универсальная газовая постоянная, N A — число Авогадро.
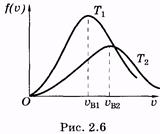
При увеличении температуры максимум кривой Максвелла смещается в сторону больших скоростей и распределение молекул по u видоизменяется (рис. 2.6; Т1 < Т2). Распределение Максвелла позволяет вычислить число молекул, скорости которых лежат в определенном интервале Du. Получим соответствующую формулу.
Так как общее число N молекул в газе обычно велико, то вероятность d P может быть выражена как отношение числа d N молекул, скорости которых заключены в некотором интервале du, к общему числу N молекул:
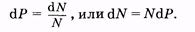 |
(2.37)
Из (2.34) и (2.37) следует, что
 |
(2.38)

|
|
Формула (2.38) позволяет определить число молекул, скорости которых лежат в интервале от и: до i>2. Для этого нужно проинтегрировать (2.38):
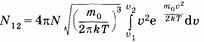
|
(2.39)
либо графически вычислить площадь криволинейной трапеции в пределах от u1 до u 2 (рис. 2.7).
Если интервал скоростей du достаточно мал, то число молекул, скорости которых соответствуют этому интервалу, может быть рассчитано приближенно по формуле (2.38) или графически как площадь прямоугольника с основанием du.
На вопрос, сколько молекул имеют скорость, равную какому-либо определенному значению, следует странный, на первый взгляд, ответ: если совершенно точно задана скорость, то интервал скоростей равен нулю (du = 0) и из (2.38) получаем нуль, т. е. ни одна молекула не имеет скорости, точно равной наперед заданной. Это соответствует одному из положений теории вероятностей: для непрерывной случайной величины, каковой является скорость, невозможно «угадать» совершенно точно ее значение, которое имеет по крайней мере хотя бы одна молекула в газе.
Распределение молекул по скоростям подтверждено различными опытами.
Распределение Максвелла можно рассматривать как распределение молекул не только по скоростям, но и по кинетическим энергиям (так как эти понятия взаимосвязаны).
Распределение Больцмана. Если молекулы находятся в каком-либо внешнем силовом поле, например гравитационном поле Земли, то можно найти распределение по их потенциальным энергиям, т. е. установить концентрацию частиц, обладающих некоторым определенным значением потенциальной энергии.
Распределение частиц по потенциальным энергиям в силовых полях — гравитационном, электрическом и др. — называют распределением Больцмана.
Применительно к гравитационному полю это распределение может быть записано в виде зависимости концентрации п молекул от высоты h над уровнем Земли или от потенциальной энергии молекулы mgh:
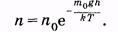 |
(2.40)
Выражение (2.40) справедливо для частиц идеального газа. Графически эта экспоненциальная зависимость изображена на рис. 2.8.

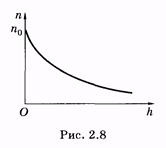
Такое распределение молекул в поле тяготения Земли можно качественно, в рамках молекулярно-кинетических представлений, объяснить тем, что на молекулы оказывают влияние два противоположных фактора: гравитационное поле, под действием которого все молекулы притягиваются к Земле, и молекулярно-хаотическое движение, стремящееся равномерно разбросать молекулы по всему возможному объему.
В заключение полезно заметить некоторое сходство экспоненциальных членов в распределениях Максвелла и Больцмана:
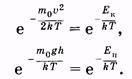
В первом распределении в показателе степени отношение кинетической энергии молекулы к kT, во втором — отношение потенциальной энергии к kT.
|
|
|
Дата добавления: 2014-01-06; Просмотров: 941; Нарушение авторских прав?; Мы поможем в написании вашей работы!