Связи и их реакции

По определению, тело, которое не скреплено с другими телами и может совершать из данного положе­ния любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.

Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так.

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равнове­сии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Рассмотрим, как направлены реакции некоторых основных видов связей.

1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпен­дикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.14, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям сопри­касающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 14, б), то реакция направлена по нормали к другой поверх­ности.

Если поверхности не гладкие, надо добавить еще одну силу – силу трения 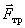, которая направлена перпендикулярно нормальной реакции 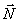в сторону, противоположную возможному скольжению тела.

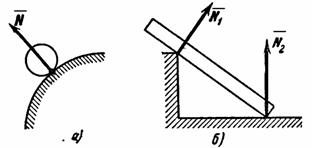
Рис.14 Рис.15

Рис.16

2. Нить. Связь, осуществленная в виде гибкой нерастяжимой нити (рис.15), не дает телу М удаляться от точки подвеса нити по направлению AM. Поэтому реакция Т натянутой нити направлена вдоль нити от тела к точке ее подвеса. Если даже заранее можно догадаться, что реакция направлена к телу, все равно ее надо направить от тела. Таково правило. Оно избавляет от лишних и ненужных предположений и, как убедимся далее, помогает установить сжат стержень или растянут.

3. Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром; осевая линия болта называется осью шарнира. Тело АВ, прикреплен­ное шарниром к опоре D (рис.16, а), может поворачиваться как угодно вокруг оси шарнира (в плоскости чертежа); при этом конец А тела не может переместиться ни по какому направлению, перпен­дикулярному к оси шарнира. Поэтому реакция R цилиндрического шарнира может иметь любое направление в плоскости, перпен­дикулярной к оси шарнира, т.е. в плоскости А _ху. Для силы R в этом случае наперед не известны ни ее модуль R, ни направле­ние (угол ).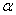

4. Шаровой шарнир и подпятник. Этот вид связи закреп­ляет какую-нибудь точку тела так, что она не может совершать никаких перемещений в пространстве. При­мерами таких связей служат шаровая пята, с помощью которой прикрепляется фото­аппарат к штативу (рис.16, б) и подшипник с упором (подпятник) (рис. 16, в). Реакция R шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее наперед неизвестны ни модуль реакции R, ни углы, образуемые ею с осями х, у, z.

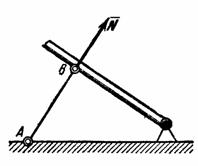
Рис.17

5. Стержень. Пусть в какой-нибудь конструкции связью является стержень АВ, закрепленный на концах шарнирами (рис.17). Примем, что весом стержня по сравнению с воспринимаемой им нагрузкой можно пре­небречь. Тогда на стержень будут действовать только две силы при­ложенные в шарнирах А и В. Но если стержень АВ находится в равновесии, то по аксиоме 1 приложенные в точках А и В силы должны быть направлены вдоль одной прямой, т. е. вдоль оси стержня. Следовательно, нагруженный на концах стержень, весом ко­торого по сравнению с этими нагрузками можно пренебречь, работает только на растяжение или на сжатие. Если такой стержень является связью, то реакция 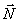стержня будет направлена вдоль оси стержня.

6. Подвижная шарнирная опора (рис.18, опора А) препятствует движению тела только в направ­лении перпендикулярном плоскости скольжения опоры. Реакция такой опоры направлена по нормали к поверхности, на которую опираются катки подвижной опоры.

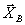7. Неподвижная шарнирная опора (рис.18, опора В). Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа. При решении задач будем реакцию изображать ее составляющими и 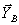по направлениям осей координат. Если мы, решив задачу, найдем 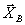и 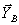, то тем самым будет определена и реакция ; по модулю

Рис.18

Способ закрепления, показанный на рис.18, употребляется для того, чтобы в балке АВ не возникало дополнительных напряжений при изменении ее длины от изменения температуры или от изгиба.

Заметим, что если опору А балки (рис.18) сделать тоже непо­движной, то балка при действии на нее любой плоской системы сил будет статически неопределимой, так как тогда в три уравнения равновесия вой­дут четыре неизвестные реакции , , , .

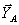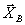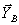8. Неподвижная защемляющая опора или жесткая заделка (рис.19). В этом случае на заделанный конец балки со стороны опорных плоско­стей действует система распределенных сил реакций. Считая эти силы приведен­ными к центру А, мы можем их заменить одной наперед неизвестной силой , приложенной в этом центре, и парой с наперед неизвестным моментом . Силу можно в свою очередь изобразить ее составляющими и 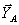. Таким образом, для нахождения реакции неподвижной защемляющей опоры надо определить три неизвестных величины , 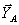и . Если под такую балку где-нибудь в точке В подвести еще одну опору, то балка станет статически неопределимой.

Рис.19

При определении реакций связи других конструкций надо установить, разре­шает ли она двигаться вдоль трех взаимно перпендикулярных осей и вращаться вокруг этих осей. Если препятствует какому-либо движению – показать соот­ветствующую силу, если препятствует вращению – пару с соответствующим моментом.

Иногда приходится исследовать равновесие нетвердых тел. При этом будем пользоваться предположением, что если это нетвердое тело находится в равновесии под действием сил, то его можно рассматривать как твердое тело, используя все правила и методы статики.

Пример 1. На невесомую трехшарнирную арку действует горизонтальная сила (рис.20). Определить линию действия реакции 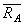(реакции связи в точке А).

Решение: Рассмотрим правую часть арки отдельно. В точках В и С приложим силы реакции связе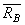й и . Тело под действием двух сил находится в равновесии. Согласно аксиоме о равновесии двух сил, силы 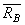и равны по величине и действуют вдоль одной прямой в противоположные стороны. Таким образом, направление силы нам известно (вдоль линии ВС).

Рис.20

Рассмотрим левую часть арки отдельно. В точках А и С приложим силы реакции связей 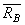и . Сила , действие равно противодействию. На тело действуют три силы, направления двух сил ( и .) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила 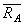направлена вдоль линии AD.

Пример 2. Однородный стержень закреплен шарнирно в точке А и опирается на гладкий цилиндр. Определить линию действия реакции 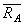(реакции связи в точке А).

Рис.21

Решение: Так как стержень однородный, то равнодействующая сил тяжести (сила ), действующих на стержень, приложена в его геометрическом центре (точка С). Так как стержень опирается на гладкую поверхность, то реакция связи (сила ) в точке касания (точка D) направлена по нормали к этой поверхности. На тело действуют три силы, направления двух сил ( и .) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила 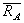направлена вдоль линии AЕ.

Дата добавления: 2014-01-06