Понятие графа

Графом G (V, E) называется совокупность двух множеств – непустого множества V (множества вершин) и множества Е его двухэлементных подмножеств множества V (Е – множество ребер).

G (V, E) = V; E, V ≠ Æ, E ⊂ 2 V

Определение 3.1.1. Граф G – это математический объект, состоящий из множества вершин X = { x ₁, x ₂,..., x_n } и множества ребер A = { a ₁, a ₂,..., a_n }. Таким образом, граф полностью определяется совокупностью множеств X, A: G = (X, A).

Для многих задач несущественно, являются ли ребра отрезками прямых или криволинейными дугами; важно лишь то, какие вершины соединяет каждое ребро.

Существуют два основных вида графов (и множество их подвидов): ориентированные и неориентированные.

Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным. Ребра ориентированного графа называются дугами. Соответствующие вершины ориентированного графа называют началом и концом. Если направления ребер не указываются, то граф называется неориентированным (или просто графом).

Примеры неориентированных графов
Граф	Вершины	Ребра
Семья	Люди	Родственные связи
Город	Перекрестки	Улицы
Сеть	Компьютеры	Кабели
Метро	Станции	Пересадки
Листок в клеточку	Клеточки	Наличие общей границы

Примеры ориентированных графов
Граф	Вершины	Дуги
Обучение	Курсы	Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Delphi, и т.п.)
Одевание ребенка	Предметы гардероба	Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т.п.)
Организация	Сотрудники	Иерархия (начальник - подчиненный)

Пример: на рис.1.изображен неориентированный граф G = (X, A).

X = { x ₁, x ₂, x ₃, x ₄}, A = { a ₁ = (x ₁, x ₂), a ₂ = (x ₂, x ₃), a ₃ = (x ₁, x ₃), a ₄ = (x ₃, x ₄)}.

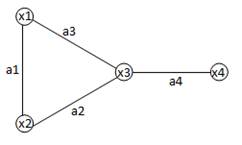рис.1

На рис.2. изображен ориентированный граф

G = (X, A).

X = { x ₁, x ₂, x ₃, x ₄},

A = { a ₁ = (x ₁, x ₂), a ₂ = (x ₁, x ₃), a ₃ = (x ₃, x ₄), a ₄ = (x ₃, x ₂)}.

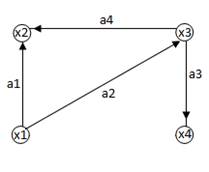рис.2

Определение 3.1.2. Граф называется простым, если каждую пару вершин соединяет не более чем одно ребро.

Определение 3.1.3. Граф, имеющий как ориентированные, так и неориентированные ребра, называется смешанным (рис.3).

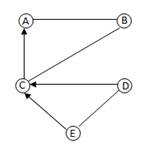рис.3

Различные ребра могут соединять одну и ту же пару вершин. Такие ребра называют кратными.

Определение 3.1.4. Граф, содержащий кратные ребра, называется мультиграфом (р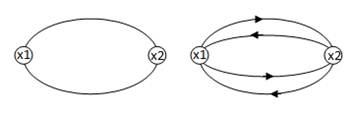ис.4).

рис.4

Неориентированное ребро графа эквивалентно двум противоположно направленным дугам, соединяющим те же самые вершины.

Ребро может соединять вершину саму с собой. Такое ребро называется петлей (рис.5).

рис.5

Определение 3.1.5. Граф с кратными ребрами и петлями называется псевдографом.

Множество ребер графа может быть пустым. Множество вершин графа не может быть пустым.

Пример. На рис.6. изображен граф

G = (X, A).

X = { a, b, c, d },

A = Æ.

рис.6

Как в случае ориентированного, так и в случае неориентированного ребра говорят, что вершины x и y инцидентны ребру a, если эти вершины соединены a.

Определение 3.1.6. Две вершины называются смежными, если они инцидентны одному и тому же ребру. Два ребра называются смежными, если они имеют общую вершину.

Определение 3.1.7. Степенью вершины графа называется число ребер, инцидентных этой вершине.

Вершина, имеющая степень 0, называется изолированной, а степень 1 – висячей.

Пример. для графа, расположенного на рис.7: d(a) = 1, d(b) = 3, d(b) = 2, d(e) = 2, d(f) = 0.

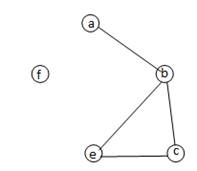рис.7

Необходимость учитывать ориентацию ребер в орграфе приводит к расщеплению понятия «степень вершины» на две части: полустепенью захода вершины v_i (d – (v_i)) называется число ребер, заходящих в v_i, полустепенью исхода v_i (d + (v_i)) – число ребер, выходящих из нее.

Определение 3.1.8. Граф, степени всех k вершин которого одинаковы, называется однородным графом степени k.

Определение 3.1.9. Дополнением данного графа называется граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф.

Для ориентированного графа множество вершин, в которые ведут дуги, исходящие из вершины х, обозначают G (х), то есть G (х) = { y:. (x,.y)∈. G }.

Множество G. (x) называют образом вершины x. Соответственно G.^{– 1}(у) – множество вершин, из которых исходят дуги, ведущие в вершину у, G.^{– 1}(y) = { x: (x, y) ∈ G }. Множество G.^{– 1}(у) называют прообразом вершины y.

Пример. В графе, изображенном на рис.8, концами ребра a ₁ являются вершины x ₁, x ₂; вершина x ₂ инцидентна ребрам a ₁, a ₂; степень вершины x ₃ равна 3; вершины x ₁ и x ₃ смежные; ребра a ₁ и a ₂ смежные; вершина x ₄ висячая. В ориентированном графе, изображенном на рис. 9, началом дуги a ₁ является вершина x ₁, а ее концом – вершина x ₂; верши на x ₁ инцидентна дугам a ₁ и a ₂; G (x 1) = { x ₂, x ₃}, G. (x ₂) = Æ, G.^{– 1}(x ₃) = { x ₁}, G.^{– 1}(x ₁) = Æ.

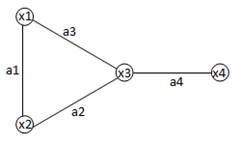рис.8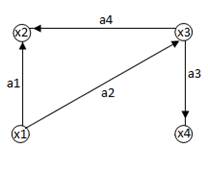рис.9

Определение 3.1.10. Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа (рис.10).

Граф	Подграфы
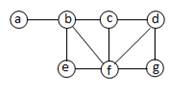
	1)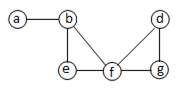	2)	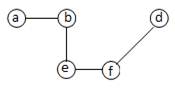3)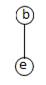

рис.10

Определение 3.1.11. Граф G = (X, A) – полный, если для любой пары вершин x_i и x_j существует ребро (x_i, x_j). Примеры полных графов рис.11.

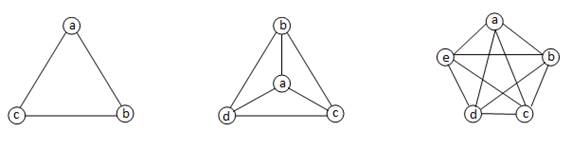рис.11

Определение 3.1.12. Полным ориентированным графом называется граф, каждая пара вершин которого соединена в точности одним ориентированным ребром. Если с каждого ребра полного ориентированного графа снять направление, то образуется полный граф с неориентированными ребрами.

Определение 3.1.13. Граф G = (X, A) – симметрический (рис.12), если для любой дуги (x_i, x_j) существует противоположно ориентированная дуга (x_j, x_i).

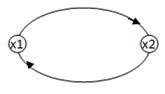рис.12

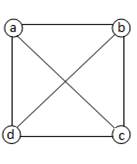
Определение 3.1.14. Граф G = (X, A) – планарный, если он может быть изображен на плоскости так, что не будет пересекающихся дуг (рис.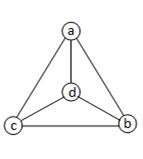13).

Рис.13

§ 3.2. Способы задания графов

Возможны следующие различные способы задания графа:

а) указанием множества вершин и множества ребер (дуг) – аналитический способ.

Пусть граф G (V, E) - рис.14 задан списком вершин и ребер:

V = {A, B, C, D, E},

E = {(A, B), (A, C), (A, D), (B, E), (A, E), (C, D)}.

б) посредством графического изображения – геометрический способ (рис.14).

Используется в случае небольшого количества ребер и вершин. При большом их числе рисунок теряет свою наглядность.

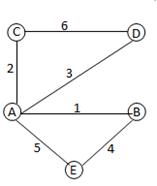рис.14

в) матрицей смежности.

Матрицей смежности ориентированного помеченного графа с вершинами называется матрица А=[a_ij] i,j =1,….n, строки которой соответствуют вершинам, а столбцы ребрам, в которой

aij=	1, если существует ребро (xi, xj)
0, если вершины xi, xj не связаны ребром

Граф

Матрица смежности

A
B
C
D
E

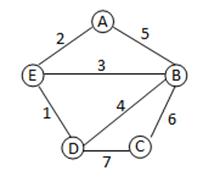
Матрица смежности однозначно определяет структуру графа. Отметим, что петля в матрице смежности может быть представлена соответствующим единичным диагональным элементом. Кратные рёбра можно представить, позволив элементу матрицы быть больше 1, но это не принято.

г) матрицей инцидентности.

Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В=[b_i,j], i=1, …, n, j=1, …, m, строки которой соответствуют вершинам, а столбцы ребрам.

bij=	1, если вершина xi инцидентна ребру uj
0, если вершина xi не инцидентна ребру uj

Матрицей инцидентности ориентированного графа с n вершинами и m ребрами называется матрица В=[b_i,j], i=1, …, n, j=1, …, m, строки которой соответствуют вершинам, а столбцы ребрам.

bij=	+1, если вершина xi начальная вершина ребра uj
-1, если вершина xi конечная вершина ребра uj
0, если вершина xi не инцидентна ребру uj

Граф

Матрица инцидентности

A
B
C
D
E

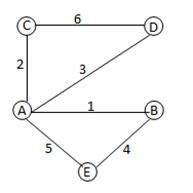
Ориентированный граф

Матрица инцидентности

A	-1		-1		-1
B				-1
C		-1
D						-1
E

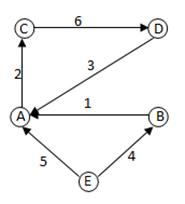
Таким образом, если граф задан одним из указанных способов: аналитическим, геометрическим или матричным, всегда можно перейти к любому другому способу задания. Наиболее часто для задания графа используется аналитический и матричный способы, а геометрический способ служит для иллюстрации полученных результатов.

Дата добавления: 2014-01-06