Эйлеровы и гамильтоновы графы

Определение 3.10.1. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом.

Определение 3.10.2. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.

Эти понятия возникли в статье Эйлера в 1735 г., в которой он решал задачу о Кенигсбергских мостах и впервые ввел понятие графа. На рис.25, а приведен план расположения семи мостов в Кенигсберге (ныне Калининграде). Задача состоит в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку С. Поскольку в конце обхода нужно вернуться в исходную часть города, и на каждом мосту нужно побывать по одному разу, этот маршрут является простым циклом, содержащим все ребра графа. В дальнейшем такие циклы и стали называть эйлеровыми, а графы, имеющие эйлеров цикл – эйлеровыми графами.

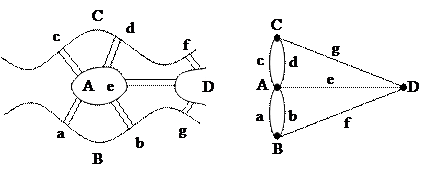рис.25

Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги. Таким образом, эйлеровы графы – это графы, которые можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной и той же точке.

Обнаружив, что в данном графе не существует циклических обходов, проходящих по всем ребрам по одному разу, Эйлер обратился к общей задаче: при каких условиях в графе можно найти такой цикл? Ответ на этот вопрос дает следующая теорема.

Теорема Эйлера. Чтобы в связанном неориентированном графе G существовал эйлеров цикл, необходимо и достаточно, чтобы число вершин нечетной степени было четным.

Определение 3.10.3. Гамильтоновой цепью графа называется его простая цепь, которая проходит через каждую вершину графа точно один раз.

Определение 3.10.4. Цикл графа, проходящий через каждую его вершину, называется гамильтоновым циклом.

Определение 3.10.5. Граф называется гамильтоновым, если он обладает гамильтоновым циклом.

Гамильтоновы графы применяются для моделирования многих практических задач, например, служат моделью при составлении расписания движения поездов. Основой всех таких задач служит классическая задача коммивояжера: коммивояжер должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижения к минимуму.

Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра — связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге. Для решения задачи необходимо найти гамильтонов цикл минимального общего веса.

Теорема Кёнига. В полном конечном графе всегда существует гамильтонов путь.

Если в графе G(X) с n вершинами для любой пары вершин x_i и x_j справедливо неравенство

m(х_i) + m(x_j) ³ n - 1,

где m(х_i), m(x_j) – степени вершин х_i и x_j, то граф G(X) имеет гамильтонову цепь.

Несмотря на сходство в определении эйлерова и гамильтонового циклов, соответствующие теории для этих понятий имеют мало общего. Критерий существования для эйлеровых циклов был установлен просто, для гамильтоновых циклов никакого общего правила неизвестно. Более того, иногда даже для конкретных графов бывает трудно решить, можно ли найти такой цикл. В принципе, поскольку речь идет о конечном числе вершин, задачу можно решить перебором, однако эффективного алгоритма неизвестно.

Дата добавления: 2014-01-06