
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задач
|
|
|
|
Задача 1. Четырем студентам (Иванову, Петрову, Семенову и Захарову) поручено от имени группы выбрать подарок девушке Алисе на день рождения (Захаров — староста группы, в случае равного разделения голосов его голос решающий). После долгих споров ребята остановились на четырех предметах:
плюшевый медведь — П.М.;
МП3 — плеер —МП3;
коробка конфет — К.К.;
парфюмерный набор — П.Н..
При обсуждении выяснилось, что по отношению к этим предметам у каждого из ребят своя система предпочтений. Системы эти представляют собой полные ориентированные графы с четырьмя вершинами (рис. 26). Стрелка от одной вершины к другой обозначает, что первая вершина предпочтительнее второй. Например, стрелка от МП3 к П.М. на рисунке 26 (а) обозначает, что Иванов при сравнении плюшевого медведя и МП3-плеера предпочитает МП3-плеер. По рисункам читаем, что Иванов наибольшее предпочтение отдает коробке конфет, Петров — плюшевому медведю, Захаров — МП3-плееру, Семенов не отдает большего предпочтения ни одному, из четырех предметов.
Ребята договорились о системе выбора подарка, которая на первый взгляд не вызывает возражений. Было решено выбирать большинством голосов (каждый голосует в соответствии со своими предпочтениями) один из двух предметов в следующем порядке:
1) либо П.М., либо МП3;
2) либо предмет, получивший большинство голосов на первом шаге голосования, либо К.К.;
3) либо предмет, получивший большинство голосов на втором шаге голосования, либо П.Н.
Какой же подарок они должны выбрать при этой системе голосования? Следим по графам на рисунке 26. На первом шаге при сравнений П.М. и МП3 большинством голосов (Иванов, Семенов и Захаров) должны были выбрать МП3-плееру. На втором шаге при сравнении МП3-плеера и коробки конфет большинством голосов (Иванов, Петров и Семенов) должны были выбрать коробку конфет. На третьем шаге при сравнении коробки конфет и парфюмерного набора большинством голосов (Петров, Семенов и Захаров) должны были выбрать парфюмерный набор.
Неожиданно получается, что четверо выбирают в подарок парфюмерный набор, хотя ни один из них не отдавал этому подарку большего предпочтения. В структуре такого голосования все решил порядок, в котором сравнивались пары предметов. Чем позже предмет участвует в выборе, тем выше его шансы быть выбранным.
Если бы, например, Иванов вник в особенности системы голосования с предпочтением и ему очень хотелось бы подарить Алисе коробку конфет, то он предложил бы друзьям изменить порядок сравнения пар предметов так, чтобы коробка конфет рассматривалась только в последней паре. Тогда, какие бы пары ни сравнивались на I и II этапах голосования, будет выбрана коробка конфет.

| 
|

|  рис.26 рис.26
|
Задача 2. В одном общежитии в разных комнатах на одном этаже живут 4 друга-студента: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них учиться в университете на разных факультетах: Технологии, Славянской филологии, Художественно-графическом и Обществознания, но неизвестно, кто на каком факультете и неизвестно, кто в какой комнате. Однако, известно, что:
1) Студент факультета «Технологии» живет левее студента «Славянской филологии».
2) Студент «Художественно – графического» живет правее студента факультета «Обществознания».
3) Студент факультета «Обществознания» живет рядом со студентом «Славянской филологии».
4) Студент факультета «Технологии» живет не рядом со студентом «Славянской филологии».
5) Виктор живет правее студента факультета «Обществознания».
6) Михаил не учится на факультете «Технологии».
7) Егор живет рядом с учащимся факультета «Славянской филологии».
8) Виктор живет левее Егора
Выясните, кто на каком факультете учиться, и кто где живет?
Решение: Введем обозначения: А-Алексей, Е-Егор, В-Виктор, М-Михаил, Т-факультет«Технологии», С-факультет «Славянской филологии», Х-факультет «Художественно-графический», О-факультет «Обществознания».
Начнем в первого условия и выпишем варианты, которые удовлетворяют ему (на рисунке ниже это первая строка). Далее будем накладывать следующее условие на выбранные варианты. И так будем делать до тех пор, пока не рассмотрим все условия. На рисунке 27 описан ход решения:
 рис.27
рис.27
Задача 3. В соревнованиях по настольному теннису, проходящих по олимпийской системе, участвуют 10 спортсменов. За какое минимальное время можно провести соревнование, если в спортивном зале установлено 2 теннисных стола, и на каждую встречу, включая разминку и отдых, отводится час? Изобразите схему соревнований с помощью корневого дерева.

Минимум 5 часов необходимо, чтобы провести соревнования.
Задача 4. Необходимо составить фрагмент расписания для одного дня с учетом следующих обстоятельств:
1. учитель истории может дать либо первый, либо второй, либо третий уроки, но только один урок;
2. учитель литературы может дать один, либо второй, либо третий урок;
3. математик готов дать либо только первый, либо только третий урок;
4. преподаватель физкультуры согласен дать только последний урок.
Сколько и каких вариантов расписания, удовлетворяющего всем вышеперечисленным условиям одновременно, может составить завуч школы?
Решение. Без сомнения, эту задачу можно решить путем обыкновенного перебора всех возможных вариантов, но решение будет наиболее простым, если вычертить граф. Требуемый граф изображен на рисунке 28.
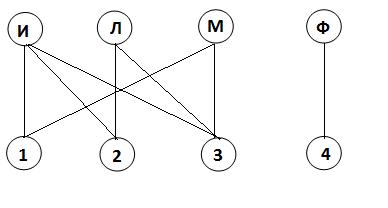 рис.28
рис.28
Итого получается три возможных варианта расписания уроков:
| История | Математика | Математика | |
| Литература | История | Литература | |
| Математика | Литература | История | |
| Физкультура | Физкультура | Физкультура |
Задания для самостоятельной работы
Задание 1. Могут ли существовать графы, у которых n вершин и степени которых равны:
а) n = 5; d(1) = 6, d(2) = 4, d(3) = 4, d(4) = 3, d(5) = 1;
б) n = 6; d(1) = 6, d(2) = 3, d(3) = 3, d(4) = 3, d(5) = 1, d(6) = 1;
в) n = 5; d(1) = 4, d(2) = 3, d(3) = 2, d(4) = 1, d(5) = 1;
г) n = 5; d(l) = 4, d(2) = 3, d(3) = 2, d(4) = 2, d(5) = 1;
д) n = 6; d(l) = 4, d(2) = 3, d(3) = 3, d(4) = 3, d(5) = 1, d(6) = 1;
е) n = 6; d(1) = 4, d(2) = 3, d(3) = 3, d(4) = 3, d(5) = 2, d(6) = 1;
ж) n = 7; d(1) = 6, d(2) = 4, d(3) = 3, d(4) = 3, d(5) = 3, d(6) = 3, d(7) =1;
Задание 2. Покажите, что два графа на рисунке изоморфны.
 Рис.29
Рис.29
Задание 3. Среди приведенных на рисунке графов найдите все пары изоморфных графов:
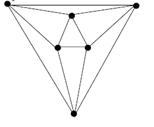 а) а)
| 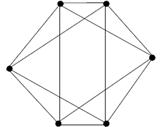 б) б)
|  в) в)
|
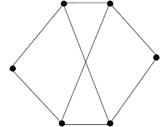 г) г)
| 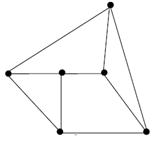 д) д)
| 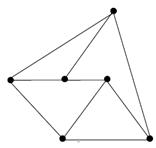 е) е)
|
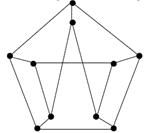 ё) ё)
|  ж) рис.30 ж) рис.30
|
Задание 4. Какие из графов, изображенных на рисунке, являются планарными?
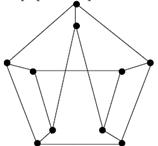 а) а)
| 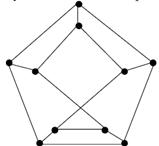 б) б)
|
 в) в)
| 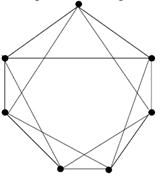 г) г)
|
Рис.31
Задание 5. Указать какие из графов, которые изображены на рисунках являются псевдографами, мультиграфами. простыми графами.
 а) а)
| 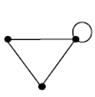 б) б)
| 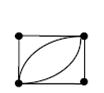 в) в)
|
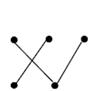 г) г)
|  д) д)
|
Рис.32
Задание 6. Для графа, изображенного на рисунке, найдите:
а) матрицу смежности (вершин);
б) матрицу инциденций.
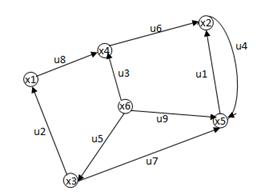 Рис.33 Рис.33
|
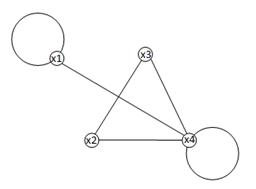
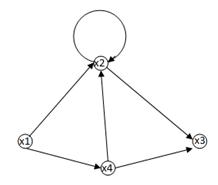
Задание 7. Найти степени вершин x1, x2, x3, x4 графа G1 и полустепени исхода и захода вершин x1, x2, x3, x4 графа G2 изображенных на рисунках:
| G1 | G2 |
| 
|
Рис.34
Задание 8. Превратите каждый из графов, изображенных на рисунке, в два разных ориентированных графа и укажите число полустепеней захода и полустепеней исхода их вершин.
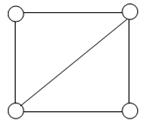
 Рис.35
Рис.35
Задание 9. Даны два графа 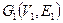 ,
, 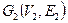
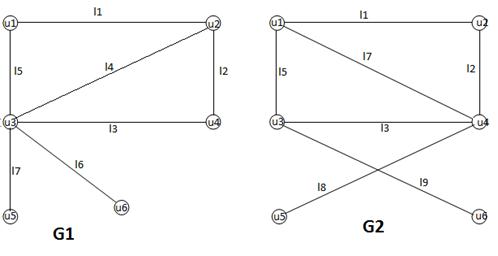 Рис.36
Рис.36
Изобразите геометрически объединение графов 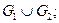 пересечение графов
пересечение графов 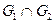 и сумму по модулю два
и сумму по модулю два 
Задание 9. Одиннадцать школьников, уезжая на каникулы, договорились, что каждый из них пошлет открытки трем из остальных. Может ли оказаться так, что каждый получит открытки именно от тех, кому напишет сам?
Задание 10. В классе 12 мальчиков и 16 девочек. Каждая девочка дружит ровно с 3 мальчиками. Количество девочек, с которыми дружат мальчики одинаково. Со сколькими девочками дружит каждый мальчик?
Задание 11. На математической олимпиаде каждый из трех призеров решил ровно 6 задач. Известно, что каждую задачу решило ровно 2 призера. Сколько было задач?
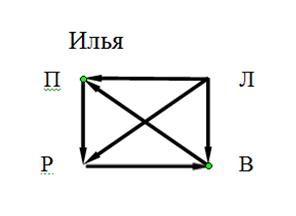
Задание 12. 4 друга (Илья, Андрей, Петр, Борис) хотят поехать вместе отдыхать. После обсуждения всех возможных мест для поездки они остановились на четырех вариантах: Прага (П), Лондон (Л), Рим (Р), Вена (В). У каждого из друзей есть свои предпочтения при выборе места отдыха (см. рис.). Они договорились о следующей схеме голосования:
1) П или Л;
2) результат (1) или Р;
3) результат (2) или В.
Куда поедут отдыхать друзья в этом году? Может ли измениться цель поездки при изменении порядка голосования? Существует ли возможность поехать в Прагу при каком либо из вариантов выбора порядка голосования?
| 
|

| 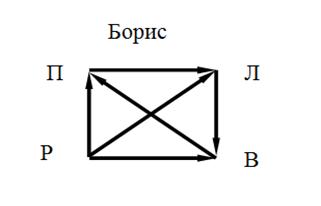 рис.37 рис.37
|
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 4895; Нарушение авторских прав?; Мы поможем в написании вашей работы!