Некоторые понятия теории вероятностей, применяемые при испытаниях ЭС

Тема №2. Основы теории испытаний электронных средств

Вопрос 6 Мировой кредитный рынок.

В силу очень большой величины этого рынка чаще всего рассматривают по частям, анализируя мировой рынок долговых ценных бумаг и мировой рынок банковских кредитов. На рынке долговых ценных бумаг обращаются прежде всего такие ценные бумаги, как векселя и облигации (частные и государственные). Примером может быть российский рынок таких бумаг. Хотя подавляющую его часть составляют векселя различных негосударственных компаний, они не пользуются спросом со стороны нерезидентов и поэтому этот сегмент российского рынка ценных бумаг слабо участвовал в деятельности мирового рынка долговых ценных бумаг. Схожая картина и с облигациями российских компаний.

На мировом рынке долговых ценных бумаг также заметное место занимают государственные ценные бумаги, а среди них - прежде всего американские, как наиболее надежные (на них приходится около половины всего мирового рынка государственных ценных бумаг общим объемом около 18 трлн. долл.). Причем в отличие от развивающихся стран и стран с переходной экономикой рынки государственных ценных бумаг в развитых странах устойчивы в силу большей стабильности экономик этих стран, их бюджетов и величины золотовалютных резервов, хотя и на этих рынках бывают приливы и отливы “горячих денег”.

В процессе испытаний ЭС приходится иметь дело со случайными событиями.

Случайное событие – которое может произойти или не произойти при определенном комплексе условий, тесно связанных с возможностью появления данного события.

На практике приходится иметь дело с показателями качества, когда результат наблюдения основан на констатации, произошло это событие или нет – качественный признак. Примеры качественных признаков: годное (хорошее) или бракованное (плохое) изделие. Другой пример: попадание параметра в пределы допусков. Эти события случайные.

Предсказать вероятность появления случайного события можно с помощью теории вероятности.

Термины и определения:

Вероятность – число, характеризующее меру возможности

наступления случайного события в результате испытания при заданной совокупности условий.

Характеристики партии (генеральной совокупности):

N – общее количество изделий;

D – число бракованных изделий;

- вероятность извлечения бракованного изделия из партии равна:

Q=D/N;

Q – величина постоянная;

Выборочные характеристики:

n – объем выборки из партии (случайный отбор);

d – число бракованных изделий в выборке (после разбраковки);

- доля бракованных изделий (частость бракованных изделий, статистическая вероятность): ;

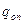- величина случайная; статистическая вероятность 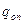при увеличении числа опытов теряет свой случайный характер и ее средняя величина приближается к генеральной характеристики Q.

Достоверное событие – оно в результате опыта должно непременно произойти (вероятность =1). Пример: извлечение годных изделий из партии, состоящей только из годных изделий.

Все другие только возможные события (вероятностью доли 1).

Практически достоверное событие – вероятность его весьма близка к 1,

Невозможное событие – оно в данном опыте не может произойти. Пример: извлечение бракованных изделий из партии, состоящей только из годных изделий.

Практически невозможное событие – вероятность его весьма близка к нулю.

Вопрос о малости практически невозможного события решается из практических соображений и важности оцениваемой задачи.

Вероятность события: число положительное и лежит в пределах 0…1.

Зная вероятность того, что событие произойдет (P), находим вероятность того, что событие не произойдет (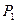):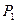=1-P.

Значение параметров качества изделий выборки – первичный статистический материал, подлежащий обработке, осмыслению и научному анализу.

Алгоритм обработки результатов наблюдений над случайной величиной х и некоторые замечания:

1. Сначала измеренные значения параметра располагаются в возрастающем или убывающем порядке – упорядоченный (ранжированный) ряд.

Пример. Измеренные значения параметра х, расположенные в возрастающем порядке.

120, 124, 126, 129, 129, 131, 132, 133, 133, 135, 135, 135, 135, ……………193, 196, 197, 200

Всего – 466 измерений, минимальное значение – 120, максимальное –

200..

Ранжированный ряд все-таки мало пригоден для дальнейшей обработки.

2. Строится статистический ряд, в котором одни и те же значения

случайной величины объединены (Табл.2.1).

Замечания (терминология):

m –абсолютная частота (статистический вес) – число случаев для каждого из повторяющихся значений;

Дискретное изменение параметра качества - лежащие рядом его значения в ранжированном ряду отличаются одно от другого на некоторую

Таблица 2.1.

х (или интервал х)	m	х (или интервал х)	m
120…124 124…128 128…132 132…136 136…140   140…144 144…148 148…152 152…156 156…160	/=1 //=2 ////=4 //////=6 ///////////=11   ////////////////=16 ///////////////////////=22 /////////……//////=40 ////////…….//////=56 ////////…….//////=69	160…164 164…168 168…172 172…176 176…180   180…184 184…188 188…192 192…196 196…200	////////////////…../////=64 ////////////////…../////=52 ////////////////…../////=41 ////////////////…../////=30 //////////////////=18   //////////////=14 /////////=9 ///////=7 //=2 //=2

конечную величину (целое число). Пример: составляющие выборки неделимые объекты.

Непрерывное изменение параметра качества - лежащие рядом его

значения в ранжированном ряду отличаются одно от другого на сколь угодно малую величину. Пример: все измерения – величина непрерывная, и зависит только от точности измерений. При непрерывном изменении параметра качества его распределение связано с интервальным распределением параметра.

Величина интервала (класса) – центральное значение (середина).

Если значение случайной величины находится в точности на границе двух интервалов, то решение куда его (и подобные значения) относить принимает исследователь. Можно рекомендовать:

– либо делить значение пополам, а половины прибавлять к верхнему и нижнему интервалам;

- либо в интервал включать те наблюдения, значения, которых больше нижней границы интервала и меньше или равны верхней.

- число интервалов, на которые следует группировать статистический материал: не должно быть слишком большим – ряд распределения становится невыразительным и частоты в нем обнаруживают незакономерные колебания; не должно быть и слишком малым – свойства распределения описываются статистическим рядом слишком грубо; рекомендуется: при достаточно большом числе наблюдений выбирать 10…20 интервалов.

Длина интервалов (ширина классов) может быть:

- одинаковой – тогда все расчеты проще, а длина интервала вычисляется по формуле:

,

где 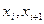- границы i – го интервала; 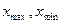- максимальное и минимальное значения; k –число интервалов;

- различной – ее удобно выбирать при формировании данных о случайных величинах, распределенных крайне неравномерно;

- в области наибольшей плотности распределения длину интервалов надо брать более узкой;

При неодинаковой длине интервалов удобнее пользоваться относительной частотой (или частостью):

,

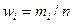где, 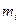- частота (i–е значение параметра), приходящаяся на i–й интервал; n – общее число наблюдений;

Сумма частостей всех интервалов = 1 (или 100%).

Численные методы представления статистического ряда

Числовые значения, представляющие статистический материал, отражают существенные характеристики

статистического ряда – характеристики положения и рассеивания случайной величины.

Важнейшие числовые характеристики статистического ряда:

характеристика положения - средняя арифметическая величина наблюдаемых значений параметра качества (или просто средняя):

характеристика выборки – выборочная средняя арифметическая и обозначается ;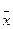

Средняя является обобщающей характеристикой только тогда, когда она применяется к однородной совокупности статистического материала;

Вычисление средней: пусть в результате n измерений имеем значения 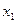,,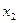…с соответствующими частотами 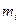и условии 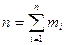, то

Выборочная средняя всегда содержит элемент случайности

Характеристика положения – медиана случайной величины: если полученные при измерениях значения расположить в возрастающем или убывающем порядке, то медиана – значение Ме, занимающее серединное значение в ряду;

Медиана – значение параметра, которое делит упорядоченный ряд на две равные по объему (по «штукам») группы.

Вычисление медианы:

при нечетном числе измерений (n=2i+1) значение параметра для случая i+1 будет медианным, т.е.

Ме=+1

при четном числе измерений (n=2i) медианой является средняя арифметическая двух значений, расположенных в середине ряда, т.е.

Ме=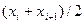

Характеристика положения – мода случайной величины – значение параметра, которое наиболее часто встречается в данном ряду: обозначается через Мо;

для дискретного ряда – мода = значению параметра с наибольшей частотой.

- Характеристика рассеивания случайной величины – размах: R =;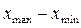

Применяется в качестве приблизительной оценки рассеивания.

Характеристика рассеивания случайной величины – выборочная дисперсия:

показывает, как тесно группируются отдельные значения вокруг средней арифметической; обозначается через .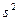

Вычисление выборочной дисперсии:

для простой статистической совокупности

при наличии частот :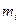

,

где .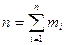

Характеристика рассеивания случайной величины – стандартное отклонение s:

имеет ту же размерность, что и средняя арифметическая ;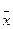

Вычисление стандартного отклонения:

;

.

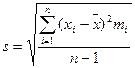Характеристика рассеивания случайной величины – коэффициент вариации V:

V = s /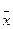100;

безразмерный;

показывает относительное колебание отдельных значений около средней арифметической.

Математическое ожидание (генеральное среднее арифметическое значение случайной величины; центр формирования значений случайной величины в генеральной совокупности):

играет роль характеристики положения случайной величины в генеральной совокупности;

случайная величина Х может принимать дискретные положения 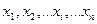с соответствующими вероятностями . На оси х положение значений случайной величины можно охарактеризовать с помощью генерального среднего арифметического значения случайной величины М(х):

,

с учетом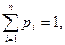

.

Математическое ожидание – величина постоянная для данной генеральной совокупности.

Дисперсия случайной величины (среднее квадратическое отклонение) Х в генеральной совокупности подсчитывают по формуле:

когда не повторяется -;

когда повторяется -;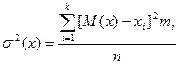

где

Распределение вероятностей появления дискретных случайных величин описывается законами: гипергеометрическим, биномиальным, Пуассона.

Распределение вероятностей появления непрерывных случайных величин описывается законами: экспоненциальным, гауссовским, Вейбулла.

Дата добавления: 2014-01-06