Ускорение точки равно первой производной по времени от скорости точки

Научимся вычислять скорость при трёх способах задания движения.

ПРИ ВЕКТОРНОМ СПОСОБЕ

Задано .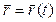

Исходя из определения ускорения, при векторном способе оно определяется соотношением:

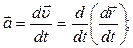
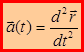(1.14)

ПРИ КООРДИНАТНОМ СПОСОБЕ

Задано:

Разложим по ортам:

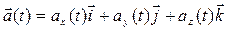(1.15)

С другой стороны, из (1.14) следует:

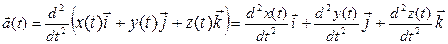, (1.16)

поскольку .

Для равенства двух векторов необходимо и достаточно, чтобы были равны их проекции. Сравнивая (1.15) и (1.16):

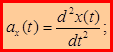
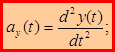
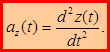(1.17)

Модуль ускорения находится по формуле:

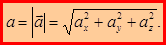или 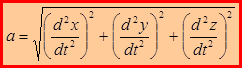(1.18)

Направляющие косинусы:

;

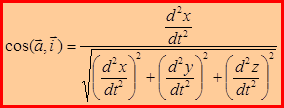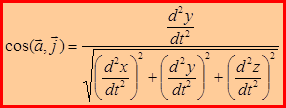; (1.19)

.

ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ

Задано S=S(t). Скорость при естественном способе задания движения 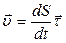. По определению ускорения:

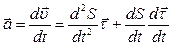. (1.20)

Направление вектора 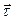зависит от значения естественной координаты S. Поскольку 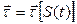, то:

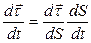. (1.21)

Подставляя (1.21) в (1.20):

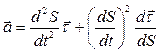(1.22)

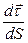– определяется лишь характером кривой линии.

Угол между касательными называют углом смежности (∆ α – угол смежности).

Выясним направление вектора 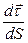. Устремим ∆S → 0. Проведем плоскость через 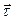и точку М’. Будем приближать точку М’ к точке М. Указанная плоскость при этом будет поворачиваться и в пределе займёт некоторое положение, которое называется соприкасающейся плоскостью.

Вектор и лежит в соприкасающейся плоскости. Он направлен в сторону вогнутости кривой. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Найдем модуль :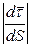

.

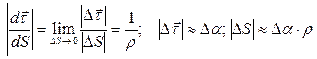Отсюда 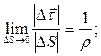где ρ – радиус кривизны траектории в рассматриваемой точке М. 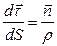, где 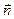– единичный вектор главной нормали, направлен в сторону вогнутости траектории.

После подстановки в (1.22):

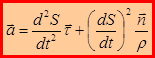(1.23)

Составляющие ускорения определяют как:

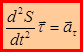– тангенциальное ускорение.

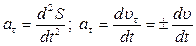– данный результат получен с учетом (1.12).

Если 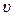=const, то 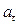= 0, следовательно 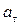– отвечает за изменение модуля скорости; 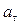= 0 – только при равномерном движении (движение при 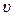=const); 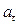– к форме траектории никакого отношения не имеет.

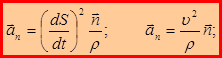– нормальное ускорение.

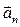Нормальное ускорение определяет форму траектории и направлено в сторону вогнутости кривой. При прямолинейном движении → ∞ и =0.

Дата добавления: 2014-01-06