Понятие волновой функции

Важнейшими характеристиками любой волны являются ее длина, частота и амплитуда. Для материальных частиц квантовая механика согласно формуле де Бройля (13.2.1) устанавливает соотношение между длиной волны и импульсом p=mv:

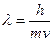. (13.2.1)

В квантовой механике амплитуду, например, электронной волны называют волновой функцией Y. С помощью волновой функции Y описывается положение электрона в атоме.

Интерпретировать волновую функцию Y можно как способ задания в любой точке пространства и в любой момент времени амплитуды «волны материи», подобно тому, как вектор напряженности электрического поля 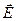задает амплитуду электромагнитной волны. Однако возможна и другая интерпретация, основанная на корпускулярно-волновом дуализме. Воспользуемся здесь аналогией со светом.

Известно, что интенсивность I любой волны пропорциональна квадрату ее амплитуды. Таким образом, получается, что число фотонов пропорционально квадрату напряженности электрического поля:

I ~ E² (13.2.3)

Если мы имеем дело только с одним фотоном, то можно интерпретировать так: в любой точке квадрат напряженности электрического поля характеризует вероятность того, что фотон находится в данном месте.

С точки зрения корпускулярной теории интенсивность светового потока пропорциональна числу фотонов N, проходящих через единичную площадку в единицу времени:

I ~ N (13.2.2)

Аналогичную интерпретацию можно использовать и в случае волн материи. Если зависящая от времени и от точки пространства волновая функция Y описывает отдельный электрон (скажем, в атоме), то определяет вероятность найти электрон в этой точке пространства в выбранный момент времени, то есть вероятность нахождения электрона в заданной точке определяется соотношением:

(13.2.4)

Для понимания корпускулярно – волнового дуализма воспользуемся данными эксперимента с двумя щелями (рис.13.3). Предположим, что ширина каждой из щелей и расстояние между ними по порядку величины сравнимы с длиной волны, падающей на них. Причем это справедливо для световой волны или дебройлевской волны электронов. В случае световой волны известно, что на экране позади щелей будет наблюдаться интерференционная картина. Удивительно, что если вместо света взять электроны, то они тоже создадут интерференционную картину. Там, где волновая функция Y обращается в ноль, находится минимум интерференционной картины. Там, где волновая функция Y максимальна, наблюдается максимум интерференционной картины. Таким образом, электрон можно рассматривать как световую волну, движущуюся одновременно через две щели, которая после прохождения щелей интерферирует между собой.

Рис. 13.3. Эксперимент с двумя щелями.

Суть всего сказанного сводится к следующему. Если мы трактуем электроны (или какие-либо другие частицы) как волны, то волновая функция Y описывает амплитуду соответствующей материальной волны. Если же мы трактуем электроны как частицы, то Y следует интерпретировать на основе вероятности нахождения электрона в заданной точке. Для двух электронов, движущихся через разные щели, справедливо сложение волн, как это происходит в случае интерференции световых волн:

. (13.2.5)

Откуда:

, (13.2.6)

где А₁ и А₂ – амплитуда волн, ответствующих первому и второму электронам, 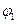и 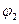- разность фаз обоих волн.

Вклад Шредингера в развитие квантовой теории заключается в том, что он предложил уравнение, которое позволяет вычислять волновую функцию. Это уравнение внешне похожее на закон сохранения механической энергии. Здесь используется волновая функция (амплитуда волны материи), описывающая вероятность нахождения частицы в данном месте в данный момент времени:

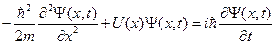(13.2.7)

где U(x) – потенциальная энергия частицы. В такой форме записи уравнение Шредингера называют нестационарным.

Слагаемое справа от знака равенства в (13.2.7) по смыслу имеет некоторое сходство с работой сил трения. Первое слагаемое слева от знака равенства напоминает кинетическую энергию частицы, а второе – потенциальную энергию.

Волновое уравнение Шредингера (13.2.7) считается основным уравнением при описании нерелятивистских материальных частиц. Оно учитывает зависимость характеристик системы от времени.

Для свободно движущейся частицы функция 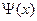не зависит от времени, а уравнение Шредингера имеет вид:

. (13.2.8)

Такое уравнение Шредингера называют стационарными.

Как видим, оно похоже на уравнение, описывающее колебания грузика на пружинке. Только изменяется в нем не координата, а вероятность нахождения частицы в заданной точке пространства. Дифференцирование в (13.2.8) осуществляется не по времени, а по пространственной координате.

При движении частицы с энергией Е в потенциальном поле U(x) уравнение Шредингера приобретает вид:

(13.2.9)

Дата добавления: 2014-01-06