Основное уравнение молекулярно-кинетической теории

Основное уравнение молекулярно-кинетической теории идеального газа[9]устанавливает связьмежду микроскопическим и макроскопическим подходом при описании состояния газа. Фактически оно устанавливает те же закономерности, что уравнения газового состояния и Клапейрона – Менделеева. Уравнение молекулярно – кинетической теории имеет вид:

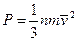, (6.5.1)

или

, (6.5.2)

где W_к =- кинетическая энергия молекул идеального газа, 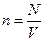- число молекул в единице объема.

Это уравнение связывает между собой макроскопический параметр давление с массой молекул и их среднеквадратичной скоростью .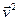

Для вывода формулы (6.5.1) запишем второй закон Ньютона для проекции на одну из осей координат ось Х:

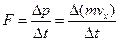, (6.5.3)

где l – длина свободного пробега. В принципе, выбирать можно любую из осей координат, поскольку в силу однородности пространства они равноправны.

Как видно на рис.6.12, изменение импульса вдоль оси Х в результате упругого соударения со стенкой сосуда (при абсолютно упругом ударе импульсы частицы до и после столкновения со стенкой равны друг другу) составляет:

,

а путь, пройденный молекулой до и после соударения со стенкой:

,

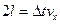следовательно

.

Рис.6.12. К выводу уравнения молекулярно-кинетической теории.

Уравнение (6.5.3) приобретает вид для одной молекулы газа:

.

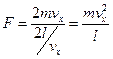Для N молекул, движущихся вдоль оси Х, сила, действующая на стенку, составит:

, (6.5.4)

где - среднеквадратичная скорость молекул вдоль оси Х, а .

Учитывая, что в изотропном пространстве нет выделенных направлений, поэтому в среднем скорость молекул вдоль каждой из осей одинакова. Тогда:

. (6.5.5)

Подставляя (6.5.5) в (6.5.4) получаем выражение для среднего давления молекул на стенку:

, (6.5.6)

где V - рассматриваемый объем площадью S.

Перепишем (6.5.6) в виде:

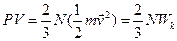, (6.5.7)

Выражения (6.4.7) и (6.5.6) согласуются, если

Это уравнение можно записать в виде:

, (6.5.6)

где k – постоянная Больцмана, причем k=1.38×10^-23 Дж/К.

Отсюда, учитывая выражение (6.5.5) следует, что средняя энергия вдоль каждой из пространственных осей составляет:

.

Дата добавления: 2014-01-06