
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция№17 Неинерциальные системы отсчета. Силы инерции. Силы инерции в неинерциальной системе отсчета, которая равномерно вращается. Центробежная сила инерции
|
|
|
|
Системы отсчета, движущиеся ускоренно относительно одной из инерциальных систем, называются неинерциальными. Они связаны с телами отсчета, находящимися во взаимодействии с внешними (по отношению к системе) телами.
Рассмотрим, как различается характер движения тел относительно инерциальной системы и системы неинерциальной, перемещающей прямолинейно и ускоренно относительно первой. Как и в случае инерциальных систем,
 (1)
(1)
Но теперь  — некоторая функция времени.
— некоторая функция времени.
Дифференцируя по t получим:
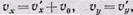
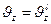 (2)
(2)
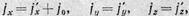 (3)
(3)
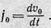
В этом случае не только скорости тела, но и ускорения его в обеих системах различны:
 (4)
(4)
Абсолютная скорость равна геометрической сумме относительной и переносной скоростей.
Абсолютное ускорение равно геометрической сумме относительного и переносного ускорений.
Пример. Пусть корабль движется параллельно линии берега с ускорением j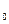 Если тело покоится на палубе корабля, то относительно берега оно движется с переносной скоростью, равной скорости движения корабля,
Если тело покоится на палубе корабля, то относительно берега оно движется с переносной скоростью, равной скорости движения корабля,  и, поскольку эта скорость изменяется, обладает переносным ускорением
и, поскольку эта скорость изменяется, обладает переносным ускорением  . Если само тело перемещается по палубе со скоростью
. Если само тело перемещается по палубе со скоростью 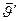 и ускорением
и ускорением  ,то перемещение относительно берега происходит со скоростью и ускорением
,то перемещение относительно берега происходит со скоростью и ускорением

Этот результат, полученный для прямолинейного поступательного переносного движения, справедлив для любого поступательного переносного движения, поскольку перемещение в этом случае может быть заменено суммой элементарных прямолинейных перемещений.
Составим уравнение движения точки массой m относительно подвижной системы отсчета 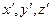 . Положим ускорение точки относительно неподвижной системы равным
. Положим ускорение точки относительно неподвижной системы равным 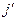 , а действующую силу равной F. Тогда для неподвижной системы в соответствии со вторым законом Ньютона
, а действующую силу равной F. Тогда для неподвижной системы в соответствии со вторым законом Ньютона
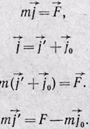 (5)
(5)
Второй закон Ньютона в системах отсчета, движущихся с ускорением, в число сил, действующих на тело, включает взятое с обратным знаком произведение массы тела на переносное ускорение.
Это произведение, учитывающее ускоренное движение системы отсчета, носит название силы инерции. Для составления уравнений движения тела относительно системы отсчета, движущейся с ускорением, к результирующей сил, приложенных к телу, надо добавить силу инерции.
Рассмотрим несколько конкретных примеров движения тел.
На тележке, покрытой гладким стеклом, лежит шарик. Сообщим тележке ускорение 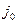 (рис. 1). Что произойдет с шариком?
(рис. 1). Что произойдет с шариком?

Рис. 1. Шарик на гладкой поверхности движущейся тележки.
В системе координат, связанной с Землей шарик остается в покое, ибо на него в направлении движения тележки не действуют никакие силы (сила трения мала, и ею можно пренебречь). Относительно тележки шарик перемещается с ускорением 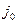
В системе координат, связанной с тележкой, шарик приобретает ускорение, хотя на шарик при этом никакие силы не действуют. Наблюдение за движением шарика позволяет нам сделать заключение, что система отсчета движется с ускорением, и при составлении уравнения движения шарика необходимо считать, что на него
действует сила инерции: F=-m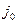 , откуда ускорение шарика относительно тележки:
, откуда ускорение шарика относительно тележки: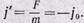
Положим, что в лифте на пружинных весах подвешен груз массой т. На него действуют сила тяжести mg, направленная вниз, и упругая сила R со стороны растянутой пружины, направленная вверх. Так как векторы сил направлены по одной прямой, то, приняв ее за ось координат, мы можем оперировать с модулями указанных векторов. Под действием уравновешивающих друг друга сил G=mg и R груз находится в покое.
Если лифт начал двигаться с ускорением 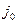 , направленным вверх, то точка прикрепления пружины начнет двигаться вверх с тем же ускорением. Вследствие инерции витки пружины и груз движутся вначале с ускорением меньшим, чем ускорение лифта. Поэтому пружина несколько растянется, груз сместится вниз, после чего приобретет ускорение, равное ускорению лифта. В инерциальной системе отсчета, связанной с Землей (скажем, относительно стенок шахты лифта), груз приобретает ускорение
, направленным вверх, то точка прикрепления пружины начнет двигаться вверх с тем же ускорением. Вследствие инерции витки пружины и груз движутся вначале с ускорением меньшим, чем ускорение лифта. Поэтому пружина несколько растянется, груз сместится вниз, после чего приобретет ускорение, равное ускорению лифта. В инерциальной системе отсчета, связанной с Землей (скажем, относительно стенок шахты лифта), груз приобретает ускорение 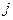 под действием разности возросшей упругой силы пружины, тянущей ее вверх, и силы тяжести G, направленной вниз. С учетом знаков сил второй закон динамики запишется в виде
под действием разности возросшей упругой силы пружины, тянущей ее вверх, и силы тяжести G, направленной вниз. С учетом знаков сил второй закон динамики запишется в виде 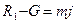

Когда груз приобретет то же ускорение, что и лифт, то
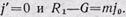
Сила натяжения пружины:
В системе отсчета, движущейся вместе с лифтом, на груз действуют сила тяжести G и упругая сила растянутой пружины 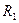 причем теперь
причем теперь 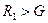 , что мы обнаруживаем по показаниям динамометра. Но хотя равенство между
, что мы обнаруживаем по показаниям динамометра. Но хотя равенство между  и G нарушено, груз, когда растяжение пружины? достигает некоторой максимальной величины, остается в покое. Следовательно, в условие равновесия груза мы должны ввести силу инерции — jom с учетом знаков:
и G нарушено, груз, когда растяжение пружины? достигает некоторой максимальной величины, остается в покое. Следовательно, в условие равновесия груза мы должны ввести силу инерции — jom с учетом знаков:

Откуда сила натяжения пружины равна:
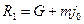
Если ускорение лифта 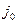 направлено вниз, то в начале движения точка подвеса приближается к грузу, который некоторое время перемещается с ускорением
направлено вниз, то в начале движения точка подвеса приближается к грузу, который некоторое время перемещается с ускорением 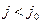 , и сила
, и сила  , действующая со стороны пружины на груз, уменьшается (так как уменьшается деформация пружины). Возникшее превышение величины силы тяжести G над величиной упругой силы
, действующая со стороны пружины на груз, уменьшается (так как уменьшается деформация пружины). Возникшее превышение величины силы тяжести G над величиной упругой силы  сообщает грузу ускорение
сообщает грузу ускорение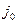 , равное ускорению лифта.Уравнение движения относительно неподвижной системы отсчета запишется на основании второго закона динамики в виде
, равное ускорению лифта.Уравнение движения относительно неподвижной системы отсчета запишется на основании второго закона динамики в виде
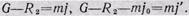
Когда груз приобретет то же ускорение, что и лифт, уравнение движения примет вид:
так как /'=0.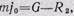
Натяжение пружины равно:

Относительно системы отсчета, связанной с лифтом, груз находится в покое, хотя вес его теперь не уравновешен упругой силой. Следовательно, вес груза частично уравновешивается силой инерции.
Откуда сила натяжения пружины равна:

Заметим, что в случае, если лифт движется с ускорением, равным ускорению свободного падения jo=g, сила натяжения пружины обращается в нуль (тело становится невесомым). Так как в неподвижной системе отсчета лифт, пружина и груз движутся с одинаковым ускорением, то не возникает их перемещений друг относительно друга, а следовательно и взаимодействий.
В системе, связанной с лифтом, наступление состояния невесомости свидетельствует о том, что переносное ускорение стало равно ускорению силы тяжести.
Таким образом, задача о движении тела относительно неинерциальной системы отсчета решается и первым и вторым способом. Принципиальной разницы между ними нет.
Отметим следующую особенность сил инерции в неинерциальных системах — особенность, которая только и отличает их от всех других сил: силы инерции не имеют противодействующей силы, так как нельзя указать тела, со стороны которого они приложены. Возникновение сил инерции также результат передачи движения, но не данному телу, а телам отсчета, относительно которых изучается движение тела.
 Рис.2
Рис.2
|
Рассмотрим диск, вращающийся вокруг перпендикулярной к нему вертикальной оси z' с угловой скоростью 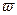 (рис. 2). Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной. Шарик занимает на спице такое положение, при котором сила натяжения пружины Fnp оказывается равной произведению массы шарика т на его ускорение wn= -
(рис. 2). Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной. Шарик занимает на спице такое положение, при котором сила натяжения пружины Fnp оказывается равной произведению массы шарика т на его ускорение wn= -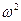 R, R — радиус-вектор, проведенный к шарику из центра диска, его модуль R дает расстояние шарика от центра диска
R, R — радиус-вектор, проведенный к шарику из центра диска, его модуль R дает расстояние шарика от центра диска  (6)
(6)
Относительно системы отсчета, связанной с диском, шарик покоится. Это можно формально объяснить тем, что, кроме силы (6), на шарик действует сила инерции направленная вдоль радиуса от центра диска.
 (7)
(7)
Силу инерции (7), возникающую во вращающейся (по отношению к инерциальным системам) системе отсчета, называют центробежной силой инерции. Эта сила действует
на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе
или движется относительно нее со скоростью v'.

|
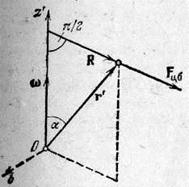
Рис.3
Если положение тела во вращающейся системе отсчета характеризовать радиусом-вектором г', центробежную силу инерции можно представить в виде двойного векторного произведения:
 (8)
(8)
Действительно, вектор b=[r', 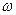 ] направлен перпендикулярно к векторам
] направлен перпендикулярно к векторам 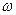 и Fu6 «на нас» (рис.3) и равен по модулю
и Fu6 «на нас» (рис.3) и равен по модулю 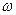 r' sin
r' sin
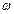 R/ Векторное произведение взаимно перпендикулярных векторов m
R/ Векторное произведение взаимно перпендикулярных векторов m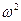 и b совпадает по направлению с Fu6 и имеет модуль, равный m
и b совпадает по направлению с Fu6 и имеет модуль, равный m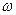 b= m
b= m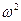 R= Fuб
R= Fuб
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 964; Нарушение авторских прав?; Мы поможем в написании вашей работы!