Энергия упругой деформации. Упругий гистерезис

Внешняя сила, перемещая части деформируемого тел а, совершает некоторую работу против внутренних сил, возникающих в теле во время деформации. При исчезновении деформации внутренние силы могут совершать работу против сил внешних. Если тело абсолютно упруго, то работа внешней силы равна работе сил внут­ренних. При деформации абсолютно упругого тела (достаточно мед­ленной, чтобы пренебречь изменением кинетической энергии) потен­циальная энергия его возрастает на величину работы, совершенной внешними силами. В реальных телах часть внутренних сил носит характер сил внутреннего трения. Поэтому работа деформирующей силы частично идет на необратимое увеличение внутренней, а не потенциальной энергии тела. Однако при деформациях, для которых справедлив закон Гука, можно считать, что вся работа внешних сил и для реальных тел идет на увеличение только их потенциальной энергии.

Подсчитаем потенциальную энергию, кото­рую приобретает пружина, растянутая на величину : силой F, пропорциональной удлинению:

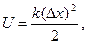
где k — коэффициент пропорциональности между силой и вызван­ным ею удлинением .

Так как в пределах применимости закона Гука коэффициент k для данного материала — величина постоянная и не зависит от ве­личины деформации, то можно написанное равенство переписать в виде

(4)

Если закон Гука не выполняется, то и в этом случае элементар­ная работа силы F, вызывающей деформацию , равна:

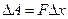, (5)

где : — достаточно малая величина деформации, при которой можно считать силу F постоянной в пределах изменения деформации от х до х+ Δ х, Выделим в деформируемом теле куб, ребро которого равно l. Тогда независимо от вида связи F=F(x) элементарная работа:

Полная работа силы F, вызвавшей деформацию :

(16)

Построим график зависимости относительной деформации от на­пряжения, откладывая по оси ординат величину ± р, по оси абсцисс (рис.6).

Рис.6

Положим, мы сообщили стержню относительное удли­нение , причем изменение напряжения р с изменением происхо­дило по кривой ОА. Когда действие внешней силы прекратится и на­пряжения станут равными нулю, то деформация в реальном теле полностью не исчезнет. При р=0 остаточная деформация равна (точка В). Если мы теперь сожмем тело, то деформация исчезнет, когда напряжение в теле приобретет некоторое значение — р₀ (точка С). Это явление называется упругим гистерезисом. Сжимая тело далее, мы достигнем некоторых значений напряжения и отно­сительной деформации, соответствующей точке А'. После прекра­щения действия сжимающей тело силы напряжение становится рав­ным нулю при относительной деформации —(точка В'). Теперь деформация тела исчезнет, если в теле возникнет напряжение +р₀ (точка С'). Вновь растягивая тело, мы попадем в точку А. При перио­дически повторяющихся деформациях графическая зависимость р от изображается, таким образом, замкнутой кривой, которая носит название петли упругого гистерезиса. Внешние силы, соответствующие участку графика В'С'А , совершают работу, пропорциональную площади, заключенной между кривой В'С'А, ординатой точки А и осью абсцисс. На участке кривой АВ работу совершают внутрен­ние силы. Она пропорциональна площади, заключенной между кри­вой АВ, ординатой точки А и осью абсцисс. Разность этих площадей, равная площади верхней части пет­ли гистерезиса, пропорциональна разности работ внешних и внутрен­них сил. Нижняя часть петли ги­стерезиса также дает разность ра­бот внешних и внутренних сил. Таким образом, площадь петли гистерезиса пропорциональна той части механической энергии, кото­рая за каждый цикл изменения на­пряжения в образце переходит во внутреннюю энергию.

Чем больше петля гистерезиса для данного материала, тем быстрее и сильнее нагревается деталь, выполненная из него, под дейст­вием переменных нагрузок. Поэтому ответственные детали машин, подвергающиеся периодическим нагрузкам (например, пружины клапанов автомобильного или авиационного двигателя), делают из специальных сортов стали, для которых петля гистерезиса мала.

Явление гистерезиса используется для ограничения величины колебаний при вибрациях. Например, для того чтобы в случае ре­зонанса амплитуда колебаний лопаток турбин под действием ударов струи не возрастала до опасной величины, лопатки изготавливаются из материалов с большой петлей гистерезиса (например, хромистые стали). Амплитуда колебаний стабилизируется и перестает расти, как только расход энергии вследствие наличия гистерезиса становит­ся равным ее поступлению.

Большое значение имеет гистерезис в процессе трения. Повто­ряющиеся при трении удары поверхностей тела создают в них перио­дически меняющиеся деформации. Так как во всех реальных телах возникают остаточные деформации (а вместе с тем и упругий гистерезис), то последний и обеспечивает при трении механизм превраще­ния механической энергии во внутреннюю энергию тела.

Дата добавления: 2014-01-06