Основное уравнение турбины

Рабочие параметры гидравлической турбины

Рабочими параметрами турбины являются:

тип турбины;

рабочий напор турбины (минимальный, максимальный и расчет-ный);

максимальная мощность турбины при расчетном напоре;

максимальный расход турбины при расчетном напоре;

КПД турбины при расчетном напоре и номинальной мощности;

номинальная частота вращения;

номинальный диаметр рабочего колеса;

высота отсасывания при расчетном напоре и максимальной мощности;

масса турбины.

По рабочим параметрам производится подбор гидротурбин при проектировании ГЭС.

6. РАБОЧИЙ ПРОЦЕСС И ХАРАКТЕРИСТИКИ ГИДРОТУРБИН

Поток жидкости, поступающий под некоторым углом на рабочее колесо турбины, меняет на рабочем колесе свое направление и уходит с него под другим углом, отличным от угла входа (рис. 6.1).

  Рис. 6.1. Схема движения потока жидкости через рабочее колесо

Выделим в этом потоке элементарную струйку, скорость которой при входе на лопастную систему v ₁, а при выходе - v ₂. Разложим скорости v ₁ и v ₂ на три составляющие - по оси турбины v_z, по радиусу v_r и направлению вращения турбины v_u. Составляющая скорости v_u создает момент количества вращения жидкости относительно оси вращения рабочего колеса L = m ^. v_u ^. r, где m - масса жидкости в струйке с центром тяжести, имеющим радиус вращения r. За время dt в межлопастное пространство рабочего

колеса по струйке войдет жидкость массой dm = 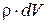, где dV - объем вошедшей жидкости. Поскольку жид-кость практически несжимаема, то за этот же промежуток времени в соответствии с уравнением неразрывности потока (2.3) из межлопастного пространства рабочего колеса по струйке выйдет такое же количество жидкости.

За счет взаимодействия струйки жидкости с лопастями рабочего колеса ее момент количества движения при входе на лопастную систему L ₁ отличается от момента количества движения при выходе из лопастной системы L ₂. Величина изменения момента количества движения dL за время dt определяется известным выражением

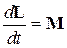, (6.1)

где М - вектор момента внешней силы относительно оси вращения. Для рассматриваемого случая выражение (6.1) можно записать в виде:

, (6.2)

где M _ст - момент силы, действующий на струйку жидкости массой dm со стороны лопасти рабочего колеса. Индексы 1 и 2 указывают на соответствие входу и выходу из рабочего колеса. Помножим обе части равенства на угловую скорость рабочего колеса 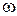. Учтем при этом, что расход струйки 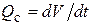, а действующий на лопасть рабочего колеса со стороны струйки момент силы M _тс = - M _ст. Тогда мощность N _тс, с которой струйка воздействует на турбину, равна

. (6.3)

Мощность элементарной струйки N _с с учетом (2.10) и (2.13) определяется выражением

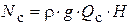, (6.4)

где H - действующий на рабочее колесо напор. Эффективность воздействия элементарной струйки на турбину характеризуется гидравлическим коэффициентом полезного действия :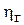

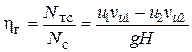, (6.5)

где u ₁ и - окружные скорости точек рабочего колеса. Выражение (6.5) можно еще представить в виде

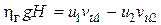. (6.6)

Поток в турбине состоит из множества элементарных струек. Если понимать под скоростями в уравнении (6.6) осредненные значения для всего потока, а под 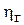- гидравлический КПД турбины, то данное уравнение справедливо для турбины в целом. Уравнение (6.6) носит название основного уравнения турбины. Впервые оно было выведено Леонардом Эйлером в 1751 г.

Дата добавления: 2014-01-06