Методологические основы адаптивного управления природно-производственным процессом. Процесс адаптации и его основные свойства

Существует три общих свойства, которые вместе характеризуют процесс адаптации.

I. Рабочие характеристики всей системы находятся под постоянным контролем и управлением.

II. Наблюдаемое поведение выражается в виде некоторого показателя качества или числовой характеристики, которые оцениваются количественно.

III. Если показатель качества изменился, то для того, чтобы он снова достиг оптимального значения, изменяются параметры устройства управления, что приводит к изменению параметров всей системы.

Следуя принципам, изложенным в [5], все адаптивные системы можно разделить на следующие типы:

- пассивные адаптивные системы, которые выполняют свои функции при значительных возмущениях управляющих параметров без изменения своей структуры;

- системы с адаптацией по выходному сигналу, изменяющие свои характеристики по входной информации;

- экстремальные системы, автоматически настраивающиеся на поиск экстремума нескольких заданных функций от заданных переменных;

- системы с адаптацией переменных, которые способны управлять набором входных переменных или преобразовывать их;

- системы с адаптацией характеристик системы с возможностью изменения функции качества системы или ее модификации.

Конечно, в определенном смысле личностное оперативное управление несет черты адаптивного управления, но стихийность этого процесса, консервативность, волюнтаризм, отсутствие системы не позволяет говорить о нем как о методике. Инерционность мышления руководителя приводит к значительному снижению эффективности управления. Изменившийся объем информации (на основании которого современный руководитель предприятия принимает решение), динамика ее изменения, возросшее число вариантов принятия решения (со значительным различием в стоимостной оценке) привели к тому, что, по нашему мнению, сумма расходов на приобретение системы адаптивного управления приблизилась к средней величине потерь при выборе неоптимального решения. Причем сумма потерь имеет тенденцию к росту, а стоимость системы адаптивного управления будет непрерывно снижаться.

Непростым является вопрос и о методах построения адаптивных управляющих систем. В ряде работ предлагаются пути построения математической модели объекта, разработки вариантов управления с целью выбора наилучшего путем подбора управляющих параметров. Имеются методы выбора лучшего варианта управления при воздействии стохастических параметров, как на весь плановый период, так и для его корректировки в узловых точках. На наш взгляд, лучшим инструментарием для построения модели является язык имитационного моделирования, позволяющий в режиме диалога с ПЭВМ найти лучший вариант управления специалисту, не имеющему специальных знаний в области программирования.

43. Основные определения имитационного динамического моделирования (уровень, темп, информационная связь).

При построении ИДМ используются следующие понятия и определения.

Шаг моделирования - это интервал времени, через который вычисляются значения всех параметров модели. Шаг моделирования обозначается DT.

Рис. 8.4. Шаг моделирования

Момент времени, предшествующий настоящему, обозначается J, настоящий момент времени - К, будущий - L. Расстояние между этими моментами времени равно DT (рис. 8.4).

На протяжении интервала времени DT все переменные модели считают неизменными, определенными в момент времени J и принимающими новые значения скачкообразно в момент времени К. Так как некоторые переменные (например, темп потока) характеризуют принятие решений, интервал времени DT иногда называют интервалом принятия решений. Имеется в виду, что решения, принятые в момент времени J (или К), определяют значения переменных, которые уже не меняются до момента времени К (или L).

Уровень - элемент, характеризующий накопление потока, достигнутый уровень (например, уровень числа рабочих, занятых в производстве, объем произведенной продукции и т.п.). Уровень изображается прямоугольником, внутри которого пишется его обозначение и номер уравнения, описывающего динамику уровня. Уровень в общем случае обозначается LEV.X, где индекс Х соответствует моменту времени, для которого берется значение уровня (X=J, К, L). Значение уровня в момент времени А равно значению уровня в момент времени J плюс (или минус) изменение уровня за период времени DT (от момента J до момента К).

Поток, вливаясь в уровень или вытекая из него, определяет изменение уровня. Обычно потоки являются материальными (например, поток рабочей силы, поток готовой продукции и т. п.). Кроме того, различают информационные потоки, с помощью которых принимается решение (определяется значение темпа потока на следующий интервал времени DT). Обычные потоки обозначаются непрерывными стрелками, информационные - пунктирными.

Поток измеряется темпом потока, характеризующим количество переносимого потоком ингредиента в единицу времени. В общем случае темп потока обозначается RT.

Рис. 8.5. Графическое изображение уровня, потока и его темпа:

а) уровень накопления субстанции; б) темп изменения субстанции;

в) истоки и конечные пункты потоков

Принимается, что темп, определенный в момент времени J (или К), остается неизменным до момента времени К (или L). Так как темп действует на протяжении временного интервала DT, время его действия обозначается двумя индексами, соответствующими началу и концу временного интервала, например RT.JK - темп, действующий на протяжении времени от J до К (рис. 8.5).

Изображение ИДМ в виде уровней и потоков, связывающих их, называют диаграммой потоков и уровней. Количество уровней определяет порядок ИДМ. Например, модель, содержащая один уровень, является одноуровневой, два - двухуровневой и т. д.

44. Системы с положительной обратной связью, их графическое и аналитическое представление.

В процессах с положительной обратной связью непрерывно поддерживается и усиливается начальное изменение какого-либо элемента контура.

Рассмотрим элементарный контур положительной обратной связи, диаграмму его потока и темпа (рис.1), его поведение и характеристики.

Рис.1. Схема элементарного контура с положительной обратной связью

ЗАДАЧА, Поток с темпом RT собирается в уровне LEV. Темп потока прямо пропорционально зависит от величины уровня, С - константа пропорциональности. В соответствии с приведенными выше правилами и обозначениями система описывается следующим уравнением:

LEV.K= LEV.J+DT×RT.JK,

где LEV.K - величина уровня в момент времени К., LEV.J - величина уровня в момент времени J; RT.JK - темп потока, вливающегося в уровень в течение интервала времени DT (от момента J до момента К).
Темп определяется в соответствии с уравнением:

RT.JK= C×LEV.J.

Подстановка выражения для темпа потока в уравнение уровня дает выражение:

LEV.K-LEV.J= DT×C×LEV.J.

Учитывая, что LEV=LEV(t) и при стремлении интервала времени DT к нулю (DT 0), можно записать:

d(LEV(t))=C×LEV(t) ×dt,

или

.

Заменяя t на и интегрируя уравнение в пределах от нуля до t, получаем:

,

получаем

или

.

Постоянная времени Т, за которое уровень возрастает в е раз, очевидно, имеет значение . Эта величина характеризует скорость роста в системе с положительной связью. Время, за которое значение уровня увеличивается вдвое, равно

.

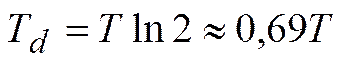График поведения RT и LEV в зависимости от времени, а также графики процессов положительной обратной связи в программной среде MathCad приведены на рис.2.

Рис.2. Графики процессов положительной обратной связи в программной среде MathCad

45. Системы с отрицательной обратной связью, их графическое и аналитическое представление.

Отрицательная обратная связь характеризуется целенаправленным поведением. Системы с отрицательной обратной связью называют также саморегулирующими, гомеостатическими, адаптирующимися и т.п. Рассмотрим элементарный контур отрицательной обратной связи (рис.1).

Рис.1. Схема элементарного контура с отрицательной обратной связью

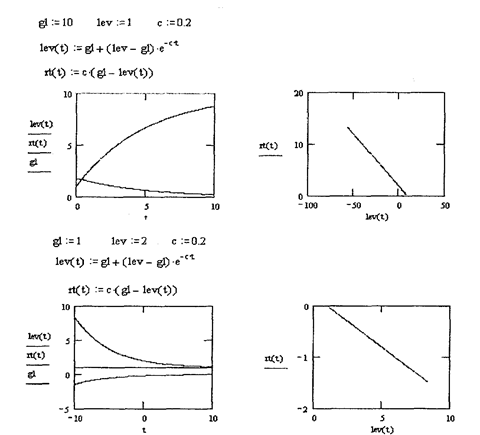
Рис.2. Графики поведения контура отрицательной обратной связи во времени,

созданные в программной среде MathCad

LEV.K=LEV.J+DT×RT.JK,

RT.JK=C×DISK.K,

где С - константа пропорциональности;

DISK.K=GL-LEV.K - разность между уровнем и целью.

Подстановка позволяет переписать систему в виде

LEV.K-LEV.J=DT×C×(GL-LEV.K),

или с учетом предельного перехода

.

Меняя t на и интегрируя в пределах от нуля до t, получаем:

или

,

откуда

.За характерное время Т = 1/ С уровень увеличивается на величину (1-1/ е) от разности между целью GL и достигнутым значением уровня:

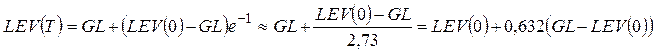. Система достигает цели примерно за время, равное 3 Т. Уровень при этом составляет примерно 0,95 GL.

Графики поведения контура отрицательной обратной связи во времени, созданные в программной среде MathCad, приведены на рис.2.

Дата добавления: 2014-01-06