Понятие покрытия

Определение. Если на каком-либо наборе f принимает значение а₁, а 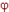– значение а₂, то говорят, что f своим значением а₁ покрывает значение а₂ функции .

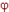При минимизации ФАЛ стремятся получить форму, в которой будет меньше букв, чем в исходной. По отношению к ДНФ эта форма называется сокращенной (Сок. ДНФ).

Смысл построения Сок. ДНФ заключается в том, что в нее входят такие элементарные произведения, которые своими единицами покрывают не одну единицу исходной функции, а несколько.

Так, каждое элементарное произведение, входящее в СДНФ, покрывает только одну единицу функции.

Например:

f(Х₁, Х₂)= Х₁Х₂ Х₁Х₂ Х₁Х₂

1 1 1

Эти единицы функции могут быть накрыты более короткими произведениями: Х₁ накрывает две единицы: Х₁Х₂ и Х₁Х₂ и Х₂, которое накрывает также две единицы: Х₁Х₂ и Х₁Х₂, т.е.

f(Х₁, Х₂)= Х₁ Х₂

ТЕОРЕМА (без док-ва):

Любая ФАЛ может быть представлена единственным образом в Сок. ДНФ, т.е. записана в виде дизъюнкции простых импликант.

Сокращенная форма не означает, что это форма является минимальной. Однако для практической реализации эта форма более удобна, чем совершенная.

Рассмотрим метод получения Сок. ДНФ, предложенный Квайном. Этот метод, и, в частности, теорема Квайна в явном и неявном виде входит практически во все методы минимизации.

Исходная форма функции – совершенная ДНФ.

ТЕОРЕМА Квайна:

Если в СДНФ в начале произвести все операции неполного склеивания, а затем все операции поглощения, то в результате получится сокращенная ДНФ.

Покажем, что, применяя операцию неполного склеивания, получим все простые импликанты функции. Введем операцию развертывания, которая обратна операции склеивания: это есть умножение каждого произведения на выражение вида (Х X)=1.

Пусть Х₁Х₂ – простая импликанта некоторой f(Х₁, Х₂, Х₃) трех переменных. Тогда:

Х₁Х₂ (Х₃Х₃)=Х₁ Х₂ Х₃ Х₁ Х₂ Х₃

получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.

В эту форму, вообще говоря, могут входить несколько одинаковых членов, т.к. разные простые импликанты могут дать одинаковые конституенты единицы. Поэтому, отбросив в ДНФ лишние члены, получим ее СДНФ.

По отношению к СДНФ применяется операция неполного склеивания, т.к. одно и то же произведение, вообще говоря, может склеиваться с несколькими другими, давая различные импликанты, то чтобы не лишиться возможности провести все операции склеивания, приходится каждое произведение, которое участвовало в операции склеивания, оставить для других операций.

Пример:

f(Х₁, Х₂)= Х₁Х₂ Х₁Х₂ Х₁Х₂ = Х₁Х₂ Х₁ или Х₁Х₂ Х₂

Таким образом после выполнения операции неполного склеивания получится не только дизъюнкция простых импликант, но и часть конституент единицы.

Если теперь провести все операции поглощения, то в полученной форме функции f останутся только простые импликанты. Покажем это. Пусть в результате операций склеивания получится член x, не являющийся простой импликантой.

Тогда x=y*z, где z – простая импликанта, которая так же должна входить в f, т.к. в нее входит x. Но z будет поглощать х, поэтому х не может входить в f. Это и доказывает теорему Квайна.

Замечание: Заметим, что теорема Квайна применяется по отношению к функции СДНФ.

Порядок получения Сок. ДНФ может быть следующим:

1. Провести все операции неполного склеивания конституент единицы исходной СДНФ. Получатся произведения (n-1) ранга; оставшиеся несклеенные конституенты единицы не могут участвовать в дальнейших склеиваниях.
2. Провести покрытие всех полученных произведений и конституент единицы. Часть некоторых конституент единицы будет устранена.
3. Продолжить, пока возможны операции 1) и 2).

Пример 1:

f(Х₁, Х₂)= Х₁Х₂ Х₁Х₂ Х₁Х₂

Если применим операцию полного склеивания, то получим:

или

f(Х₁, Х₂)= Х₁ Х₁Х₂

или

f(Х₁, Х₂)= Х₁Х₂ Х₂

т.е. у нас нет возможности далее провести операцию.

Применим теперь операцию неполного склеивания:

f(Х₁, Х₂)= Х₁ Х₁Х₂ Х₁Х₂ Х₁Х₂ Х₂ = Х₁ Х₂ Х₁Х₂ Х₁Х₂ Х₁Х₂

Простые импликанты: Х₁, Х₂

Конституенты единицы: Х₁Х₂, Х₁Х₂, Х₁Х₂

Теперь можем провести операции поглощения:

Х₁ поглощает: Х₁, Х₁Х₂, Х₁Х₂

Х₂ поглощает: Х₂, Х₁Х₂, Х₁ Х₂

Т.е. сокращенная ДНФ

f(Х₁, Х₂)= Х₁ Х₂ в данном случае она – минимальная форма.

Пример 2:

Пусть задана:

f(Х₁, Х₂, Х₃)= Х₁Х₃ Х₁Х₂ Х₁Х₂ Х₃

f(Х₁, Х₂, Х₃)= Х₁Х₃ Х₁Х₂ Х₁Х₂ Х₃

Получим СДНФ:

f= Х₁Х₃ (Х₂ Х₂)Х₁Х₂ (Х₃Х₃)Х₁Х₂ Х₃ = Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ = Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃

Теперь, имея СДНФ, можно получить сокращенную ДНФ:

f(X₁,X₂,X₃)=X₁X₂X₃X₂X₃X₁X₃

Пример 3:

f(Х₁, Х₂, Х₃)=Х₁Х₂ Х₃Х₁Х₂ Х₃Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ = Х₁Х₃ Х₂Х₃ Х₁Х₂ Х₁Х₃

Склеиваются два произведения, содержащие число переменных с отрицанием, отличающихся на единицу и расположенных соответствующим образом.

Обычно произведение, содержащее 'n' букв, называется минтермом 'n'-ранга.

Дата добавления: 2014-01-06