Распределение рабочих по среднечасовой выработке изделий

№ п/п	Рабочие IVразряда	Nп/п	Рабочие Vразряда
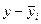
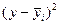
Выработка рабочего, шт., У1			Выработка рабочего, шт., У1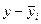
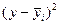
		-3				-1
2
	-1				-1
		-1
						-2
∑		-		∑		—

Для результативного признака исчислим: 1) групповые дисперсии; 2) среднюю из внутригрупповых дисперсий; 3) межгрупповую дисперсию; 4) общую дисперсию; 5)проверим правило сложения дисперсий.

В этом примере данные группируются по квалификации (тарифному разряду) рабочих, являющейся факторным признаком х.

Результативный признак у_i варьирует как под влиянием систе­матического фактора х - квалификации (межгрупповая вариация), так и других неучтенных случайных факторов (внутригрупповая вариация). Задача заключается в измерении этих вариаций с по­мощью дисперсий: общей, межгрупповой и внутригрупповых.

1. Для расчета групповых дисперсий исчислим средние вы­работки по каждой группе и общую среднюю выработку, шт.:

§ по первой группе ;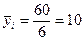

§ по второй группе ;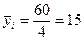

§ по двум группам

.

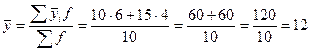Данные для расчета дисперсий по группам представлены в табл. 5.8. Подставив необходимые значения в формулу (5.32), получим внутригрупповые дисперсии:

По первой группе ;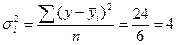

По второй группе .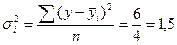

Внутригрупповые дисперсии показывают вариации выработ­ки в каждой группе, вызванные всеми возможными фактора­ми (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме различий в квалификационном разряде (внутри группы все рабочие имеют одну квалификацию).

2. Рассчитаем среднюю из внутригрупповых дисперсий (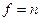) по формуле (5.34):

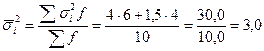
Средняя из внутригрупповых дисперсий отражает вариацию выработки, обусловленную всеми факторами, кроме квалифика­ции рабочих, но в среднем по всей совокупности.

3. Исчислим межгрупповую дисперсию по формуле (5.31):

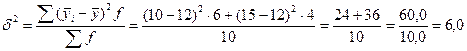
Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квали­фикационному разряду.

4. Исчислим общую дисперсию по формуле (5.20):

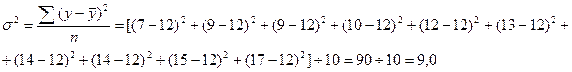
Общая дисперсия отражает суммарное влияние всех возмож­ных факторов на общую вариацию среднечасовой выработки изделий всеми рабочими цеха.

5. Суммирование средней из внутригрупповых дисперсий и
межгрупповой дает общую дисперсию:

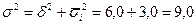
Очевидно, чем больше доля межгрупповой дисперсии в об­шей дисперсии, тем сильнее влияние группировочного признака (квалификационного разряда) на изучаемый признак (количест­во изготавливаемых изделий).

Поэтому в статистическом анализе широко используется

эмпирический коэффициент детерминации (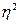) — показатель, пред­ставляющий собой долю межгрупповой дисперсии в общей дис­персии результативного признака и характеризующий силу влия­ния группировочного признака на образование общей вариации:

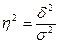. (5.36)

Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функцио­нальной связи — единице.

В нашем примере 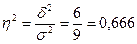(или 66,6%)

Это означает, что на 66,6% вариация производительности труда рабочих обусловлена различиями в их квалификации и на 33,4 % - влиянием прочих факторов.

Эмпирическое корреляционное отношение — это корень квад­ратный из эмпирического коэффициента детерминации:

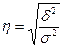, (5.37)

оно показывает тесноту связи между группировочным и ре­зультативным признаками.

Эмпирическое корреляционное отношение 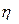, как и 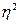, может принимать значения от 0 до 1.

Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный при­знак никак не влияет на образование общей вариации.

Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии (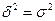), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком оп­ределяет вариацию изучаемого результативного признака.

Чем значение корреляционного отношения ближе к еди­нице, тем теснее, ближе к функциональной зависимости связь между признаками.

Для качественной оценки тесноты связи на основе показате­ля эмпирического корреляционного отношения можно восполь­зоваться соотношениями Чэддока:

ηэ 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99

Сила связи Слабая Умеренная Заметная Тесная Весьма тесная

В нашем примере 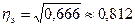, что свидетельствует о тесной связи между квалификацией рабочих и производительностью их труда.

Контрольные вопросы

1. Дайте определение средней.

2. Какова роль средних в регулировании действия случайных причин и определении среднего уровня явления?

3. В чем смысл научно обоснованного использования средних величин?

4. Какие виды средних величин применяются в статистике? Какие средние величины используются чаще всего?

5. Как исчисляется средняя арифметическая простая и в каких случаях она применяется?

6. Как исчисляется средняя арифметическая взвешенная и в каких случаях она применяется?

7. Как исчисляется средняя арифметическая из вариацион­ного ряда?

8. Почему средняя арифметическая интервального ряда являет­ся приближенной средней, от чего зависит степень ее при­ближения?

9. Каковы основные свойства средней арифметической?

10. Каков алгоритм исчисления средней арифметической из вариа­ционного ряда по способу моментов? В чем его преимущества?

11. Для чего служит средняя гармоническая? Чем она отличает­ся от средней арифметической?

12. Какие признаки называются прямыми, а какие — обратны­ми? Приведите примеры.

13. Как исчисляется средняя гармоническая простая, и в каких случаях она применяется?

14. Как исчисляется средняя гармоническая взвешенная, в каких случаях она применяется?

15. Как исчисляется средняя геометрическая, где она применяется?

16. Что представляет собой вариация признака, от чего зави­сят ее размеры?

17. Что такое размах вариации, по какой формуле он исчисля­ется, в чем его недостаток как показателя вариации?

18. Что представляет собой среднее линейное отклонение, его формулы; в чем его недостатки как показателя вариации?

19. Какой показатель вариации называется дисперсией? По ка­ким формулам она рассчитывается?

20. Что называется средним квадратическим отклонением? По каким формулам оно вычисляется?

21. Что представляет собой дисперсия альтернативного призна­ка? Чему она равна?

22. Каковы основные свойства дисперсии?

23. В чем сущность упрощенного расчета дисперсии и среднего квадратического отклонения?

24. Почему дисперсия и среднее квадратическое отклонение не всегда являются достаточными для характеристики ва­риации признака в изучаемых совокупностях?

25. Коэффициент вариации как показатель, формула его вычис­ления и значение для экономического анализа.

26. На какие две большие группы делятся причины, факторы, вызывающие вариацию признака?

27. Какая вариация называется систематической, случайной?

28. Что характеризует межгрупповая дисперсия, ее формула?

29. Как определяются внутригрупповые дисперсии, средняя из внутригрупповых дисперсий, их формулы?

30. Что собой представляет правило сложения дисперсий, в чем его практическое значение?

31. Что называется эмпирическим коэффициентом детермина­ции, каков его смысл?

32. Что называется эмпирическим корреляционным отношением, в чем его смысл?

Глава 6. Выборочный метод в статистике

6.1. Понятие о выборочном наблюдении, его задачи

Статистическое наблюдение можно органи­зовать сплошное и несплошное. Сплошное наблюдение предусмат­ривает обследование всех единиц изучаемой совокупности и связано с большими трудовыми и материальными затратами. Изуче­ние не всех единиц совокупности, а лишь некоторой части, по ко­торой следует судить о свойствах всей совокупности в целом, мож­но осуществить несплошным наблюдением. В статистической прак­тике самым распространенным является выборочное наблюдение.

Выборочное наблюдение — это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распро­страняются на всю исходную совокупность. Наблюдение организует­ся таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность.

Совокупность, из которой производится отбор, называется ге­неральной, и все ее обобщающие показатели — генеральными.

Совокупность отобранных единиц именуют выборочной сово­купностью, и все ее обобщающие показатели — выборочными.

Имеется ряд причин, в силу которых, во многих слу­чаях выборочному наблюдению отдается предпочтение перед сплошным. Наиболее существенны из них следующие:

• экономия времени и средств в результате сокращения объ­ема работы;

• сведение к минимуму порчи или уничтожения исследуемых объектов (определение прочности пряжи при разрыве, ис­пытание электрических лампочек на продолжительность горения, проверка консервов на доброкачественность);

• необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (при изучении бюджета семей);

• достижение большой точности результатов обследова­ния благодаря сокращению ошибок, происходящих при регистрации.

Преимущество выборочного наблюдения по сравнению co сплошным можно реализовать, если оно организовано и проведено в строгом соответствии с научными принципами теории выборочного метода. Такими принципами являются: обеспечение случайности (равной возможности попадания в выборку) отбора единиц и достаточного их числа. Соблюдение этих принципов позволяет получить объективную гарантию репрезентативности полученной выборочной совокупности. Понятие репрезентативности отобранной совокупности не следует понимать как ее представительство по всем признакам изучаемой совокупности, а только в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.

Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических ис­следованиях (сплошных и выборочных) возникают ошибки двух видов: регистрации и репрезентативности.

Ø Ошибки регистрации могут иметь случайный (непреднаме­ренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преувеличения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора (предвзятые цели). Их можно избежать при правильной организации и проведении наблюдения.

Ø Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная сово­купность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, по­лученных по выборке, и значениями показателей этих же вели­чин, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении, т. е. между величи­нами выборных и соответствующих генеральных показателей.

Для каждого конкретного выборочного наблюдения значе­ние ошибки репрезентативности может быть определено по со­ответствующим формулам, которые зависят от вида, метода и способа формирования выборочной совокупности.

Ø По виду различают индивидуальный, групповой и комби­нированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной со­вокупности; при групповом отборе - качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов.

Ø По методу отбора различают повторную и бесповтор­ную выборки.

При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку («отбор по схеме возвращенного шара»). Повторная выборка в социально-экономической жизни встречается редко. Обычно выборку организуют по схеме беспо­вторной выборки.

При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т. е. последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц («отбор по схеме невозвращенного шара»). Таким обра­зом, при бесповторной выборке численность единиц генераль­ной совокупности сокращается в процессе исследования.

Ø Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности.

По степени охвата единиц совокупности различают большие и малые (n <30) выборки.

В практике выборочных исследований наибольшее распространение получили следующие виды выборки: собственно-случайная, механическая, типическая, серийная, комбинированная.

Основные характеристики параметров гене­ральной и выборочной совокупностей обозначаются символами:

N – объем генеральной совокупности (число входящих в нее единиц);

п – объем выборки (число обследованных единиц);

– генеральная средняя (среднее значение признака в генеральной совокупности);

– выборочная средняя;

р – генеральная доля (доля единиц, обладающих дан­ным значением признака в общем числе единиц генеральной совокупности);

w – выборочная доля;

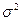– генеральная дисперсия (дисперсия признака в генеральной совокупности);

S² – выборочная дисперсия того же признака;

– среднее квадратическое отклонение в генеральной совокупности;

S – среднее квадратическое отклонение в выборке.

6.2. Ошибки выборки

При выборочном наблюдении должна быть обеспечена случайность отбора единиц. Каждая единица должна иметь равную с другими возможность быть отобранной. Именно на этом основывается собственно-случайная выборка.

К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности (без предварительного расчленения ее на какие-либо группы) посредством жеребьевки (преимущественно) или какого-либо иного подобного способа, например, с помощью таблицы случайных чисел. Случайный отбор — это отбор не беспорядочный. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо фактор, кроме случая. Примером собственно-случайного отбора могут служить тиражи выигрышей: из общего количества выпущен­ных билетов наугад отбирается определенная часть номеров, на которые приходятся выигрыши. Причем всем номерам обеспечивается равная возможность попадания в выборку, При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.

Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

.

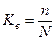Так, при 5%-ной выборке из партии деталей в 1000 ед. объ­ем выборки п составляет 50 ед., а при 10%-ной выборке — 100 ед. и т.д. При правильной научной организации выборки ошибки репрезентативности можно свести к минимальным значениям, в результате — выборочное наблюдение становится достаточно точным.

Собственно-случайный отбор «в чистом виде» применяет­ся в практике выборочного наблюдения редко, но он является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного наблюдения.

Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.

Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателей: среднюю величину ко­личественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической сово­купности, которые отличаются от всех других единиц этой сово­купности только наличием изучаемого признака).

Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности n:

w = m / п.

Например, если из 100 деталей выборки (n =100), 95 деталей оказались стандартными (т =95), то выборочная доля

w = 95 / 100 = 0,95.

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки 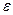или, иначе говоря, ошибка репрезента­тивности представляет собой разность соответствующих выбо­рочных и генеральных характеристик:

• для средней количественного признака

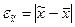; (6.1)

• для доли (альтернативного признака)

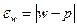. (6.2)

Ошибка выборки свойственна только выборочным наблюде­ниям. Чем больше значение этой ошибки, тем в большей степе­ни выборочные показатели отличаются от соответствующих генеральных показателей.

Выборочная средняя и выборочная доля по своей сути яв­ляются случайными величинами, которые могут принимать раз­личные значения в зависимости от того, какие единицы сово­купности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возмож­ных ошибок — среднюю ошибку выборки.

От чего зависит средняя ошибка выборки? При соблюдении принципа случайного отбора средняя ошибка выборки определяется прежде всего объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, всё более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки также зависит от степени варьирования изучаемого признака. Степень варьирования, как известно, характеризуется дисперсией 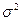или w(1 - w) — для альтернативного признака. Чем меньше вариация признака, а следовательно, и дисперсия, тем меньше средняя ошибка выборки, и наоборот. При нулевой дисперсии (признак не варьирует) средняя ошибка выборки равна нулю, т. е. любая единица генеральной совокупности будет совершенно точно характеризовать всю совокупность по этому признаку.

Зависимость средней ошибки выборки от ее объема и степе­ни варьирования признака отражена в формулах, с помощью которых можно рассчитать среднюю ошибку выборки в услови­ях выборочного наблюдения, когда генеральные характеристики (х, р) неизвестны, и следовательно, не представляется возможным нахождение реальной ошибки выборки непосредственно по формулам (6.1), (6.2).

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

§ для средней количественного признака

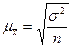; (6.3)

§ для доли (альтернативного признака)

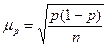. (6.4)

Поскольку практически дисперсия признака в генеральной совокупности 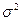точно неизвестна, на практике пользуются значением дисперсии S², рассчитанным для выборочной сово­купности на основании закона больших чисел, согласно кото­рому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики гене­ральной совокупности.

Таким образом, расчетные формулы средней ошиб­ки выборки при случайном повторном отборе будут следующие:

§ для средней количественного признака

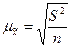; (6.5)

§ для доли (альтернативного признака)

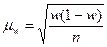. (6.6)

Однако дисперсия выборочной совокупности не равна диспер­сии генеральной совокупности, и следовательно, средние ошибки выборки, рассчитанные по формулам (6.5) и (6.6), будут прибли­женными. Но в теории вероятностей доказано, что генеральная дисперсия выражается через выборную следующим соотношением:

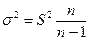. (6.7)

Так как n / (n -1) при достаточно больших n — величина, близкая к единице, то можно принять, что 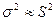, а следова­тельно, в практических расчетах средних ошибок выборки мож­но использовать формулы (6.5) и (6.6). И только в случаях ма­лой выборки (когда объем выборки не превышает 30) необхо­димо учитывать коэффициент n / (n -1) и исчислять среднюю ошибку малой выборки по формуле:

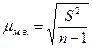. (6.8)

Ø При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подко­ренное выражение умножить на 1 - (п / N), поскольку в процес­се бесповторной выборки сокращается численность единиц ге­неральной совокупности. Следовательно, для бесповторной вы­борки расчетные формулы средней ошибки выборки примут такой вид:

§ для средней количественного признака

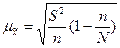; (6.9)

§ для доли (альтернативного признака)

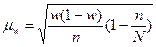. (6.10)

Так как п всегда меньше N, то дополнительный множи­тель 1 - (п /N) всегда будет меньше единицы. Отсюда следу­ет, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. В то же время при сравнительно небольшом проценте выборки этот множитель близок к еди­нице (например, при 5%-ной выборке он равен 0,95; при 2%-ной — 0,98 и т.д.). Поэтому иногда на практике пользуются для определения средней ошибки выборки формулами (6.5) и (6.6) без указанного множителя, хотя выборку и организуют как бесповторную. Это имеет место в тех случаях, когда число единиц генеральной совокупности N неизвестно или безгра­нично, или когда п очень мало по сравнению с N, и по су­ществу, введение дополнительного множителя, близкого по значению к единице, практически не повлияет на значение средней ошибки выборки.

Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, разбитой по ней­тральному признаку на равные интервалы (группы), произво­дится таким образом, что из каждой такой группы в выборку отбирается лишь одна единица. Чтобы избежать систематиче­ской ошибки, отбираться должна единица, которая находится в середине каждой группы.

При организации механического отбора единицы совокуп­ности предварительно располагают (обычно в списке) в опре­деленном порядке (например, по алфавиту, местоположению, в порядке возрастания или убывания значений какого-либо по­казателя, не связанного с изучаемым свойством, и т.д.), после чего отбирают заданное число единиц механически, через оп­ределенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки. Так, при 2%-ной выборке отбирается и проверяется каждая 50-я единица (1: 0,02), при 5 %-ной выборке — каждая 20-я едини­ца (1: 0,05), например, сходящая со станка деталь.

При достаточно большой совокупности механический отбор по точности результатов близок к собственно-случайному. По­этому для определения средней ошибки механической выборки используют формулы собственно-случайной бесповторной вы­борки (6.9), (6.10).

Для отбора единиц из неоднородной совокупности применя­ется, так называемая типическая выборка, которая используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели.

При обследовании предприятий такими группами могут быть, например, отрасль и подотрасль, формы собственности. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется при изучении слож­ных статистических совокупностей. Например, при выборочном обследовании семейных бюджетов рабочих и служащих в отдель­ных отраслях экономики, производительности труда рабочих пред­приятия, представленных отдельными группами по квалификации.

Типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц в выбороч­ную совокупность. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представи­тельство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки.

При определении средней ошибки типической выборки в ка­честве показателя вариации выступает средняя из внутригрупповых дисперсий.

§ для средней количественного признака

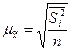(повторный отбор); (6.11)

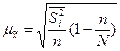(бесповторный отбор); (6.12)

§ для доли (альтернативного признака)

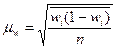(повторный отбор); (6.13)

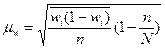(бесповторный отбор); (6.14)

где 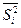- средняя из внутригрупповых дисперсий по вы­борочной совокупности;

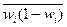- средняя из внутригрупповых дисперсий доли (альтер­нативного признака) по выборочной совокупности.

Серийная выборка предполагает случайный отбор из генераль­ной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий) с тем, чтобы в таких группах подвергать наблюде­нию все без исключения единицы.

Применение серийной выборки обусловлено тем, что многие товары для их транспортировки, хранения и продажи упаковываются в пачки, ящики и т.п. Поэтому при контроле качества упакованного товара рациональнее проверить не­сколько упаковок (серий), чем из всех упаковок отбирать не­обходимое количество товара.

Поскольку внутри групп (серий) обследуются все без исключе­ния единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.

Ø Среднюю ошибку выборки для средней количественного при­знака при серийном отборе находят по формулам:

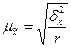(повторный отбор); (6.15)

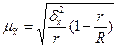(бесповторный отбор); (6.16)

где r - число отобранных серий; R - общее число серий.

Межгрупповую дисперсию серийной выборки вычисляют сле­дующим образом:

,

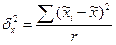где 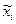- средняя i - й серии; 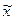- общая средняя по всей выборочной совокупности.

Ø Средняя ошибка выборки для доли (альтернативного при­знака) при серийном отборе:

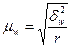(повторный отбор); (6.17)

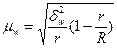(бесповторный отбор); (6.18)

Межгрупповую (межсерийную) дисперсию доли серийной вы­борки определяют по формуле:

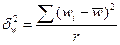, (6.19)

где 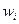- доля признака в i-й серии; 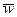- общая доля признака во всей выборочной совокупности.

В практике статистических обследований помимо рассмот­ренных ранее способов отбора применяется их комбинация (комбинированный отбор).

6.3. Распространение выборочных результатов на генеральную совокупность

Конечной целью выборочного наблюдения является ха­рактеристика генеральной совокупности на основе выбороч­ных результатов.

Выборочные средние и относительные величины распро­страняют на генеральную совокупность с учетом предела их возможной ошибки.

В каждой конкретной выборке расхождение между выбороч­ной средней и генеральной, т.е. 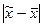может быть меньше средней ошибки выборки 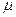, равно ей или больше ее.

Причем каждое из этих расхождений имеет различную веро­ятность (объективную возможность появления события). По­этому фактические расхождения между выборочной средней и генеральной 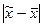можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с оп­ределенной вероятностью Р.

Предельную ошибку выборки для средней (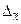) при повторном отборе можно рассчитать по формуле:

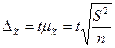, (6.20)

где t — нормированное отклонение — «коэффициент доверия», за­висящий от вероятности, с которой гарантируется предельная ошибка выборки; 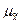— средняя ошибка выборки.

Аналогичным образом может быть записана формула пре­дельной ошибки выборки для доли 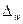при повторном отборе:

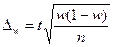. (6.21)

При случайном бесповторном отборе в формулах расчета пре­дельных ошибок выборки (6.20) и (6.21) необходимо умножить подкоренное выражение на 1 - (n / N).

Формула предельной ошибки выборки вытекает из основных положений теории выборочного метода, сформулированных в ряде теорем теории вероятностей, отражающих закон больших чисел.

На основании теоремы П.Л. Чебышева (с уточ­нениями A.M. Ляпунова) с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки и ограниченной генеральной дисперсии выборочные обобщающие показатели (средняя, доля) будут сколь угодно мало отли­чаться от соответствующих генеральных показателей.

Применительно к нахождению среднего значения признака эта теорема может быть записана так:

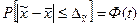, (6.22)

а для доли признака:

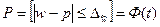, (6.23)

где 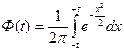. (6.24)

Таким образом, величина предельной ошибки выборки мо­жет быть установлена с определенной вероятностью.

Значения функции Ф (t) при различных значениях t как ко­эффициента кратности средней ошибки выборки, определяются на основе специально составленных таблиц. Приведем некото­рые значения (которые впоследствии будем использовать при решении задач), применяемые наиболее часто для выборок дос­таточно большого объема (п ≥30):

t 1,000 1,960 2,000 2,580 3,000

Ф(t) 0,683 0,950 0,954 0,990 0,997

Предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, значение которой оп­ределяется коэффициентом t (в практических расчетах, как правило, заданная вероятность не должна быть менее 0,95). Так, при t = 1 предельная ошибка составит 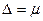, Следова­тельно, с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превы­сит одной средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ±1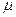. При t =2 с вероятностью 0,954 она не выйдет за пределы ±2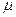, при t=3 с вероятностью 0,997 - за пределы ±3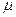и т.д.

Как видно из приведённых выше значений функции Ф (t) (см. последнее значение), вероятность появления ошибки, равной или большей утроенной средней ошибки выборки, т. е. 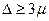, крайне мала и равна 0,003, т. е. 1—0,997. Такие маловероятные события считаются практически невозможными, а потому величину 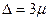можно принять за предел возможной ошибки выборки.

Выборочное наблюдение проводится в целях распростране­ния выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки исследуемых характеристик (параметров) гене­ральной совокупности.

Предельная ошибка выборки позволяет определить предель­ные значения характеристик генеральной совокупности и их дове­рительные интервалы:

§ для средней 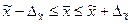; (6.25)

§ для доли 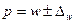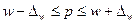; (6.26)

Это означает, что с заданной вероятностью можно утвер­ждать, что значение генеральной средней следует ожидать в пределах от 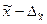до .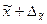

Аналогичным образом может быть записан доверительный интервал генеральной доли: ; .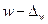

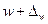Наряду с абсолютным значением предельной ошибки вы­борки рассчитывается и предельная относительная ошибка выбор­ки, которая определяется как процентное отношение предель­ной ошибки выборки к соответствующей характеристике выбо­рочной совокупности:

§ для средней, %: 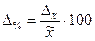; (6.27)

§ для доли, %: 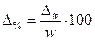. (6.28)

Рассмотрим нахождение средних и предельных ошибок вы­борки, определение доверительных пределов средней и доли на конкретных примерах.

Задача 1. Для определения скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым сред­ний срок перечисления и получения денег оказался равным 22 дням (= 22) со стандартным отклонением 6 дней (S= 6).

Необходимо с вероятностью Р = 0,954 определить пре­дельную ошибку выборочной средней и доверительные пределы средней продолжительности расчетов предприятий данной корпорации.

Решение. Предельную ошибку 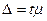определяем по формуле по­вторного отбора (6.20), так как численность генеральной совокупности N неизвестна. Из представленных значений Ф (t) (см. п. 6.3) для вероятности Р= 0,954 находим t = 2.

Следовательно, предельная ошибка выборки, дней:

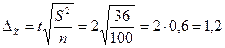
Предельная относительная ошибка выборки, %:

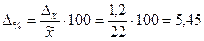
Генеральная средняя будет равна , а доверительные интервалы (пределы) генеральной средней исчисляем, исходя из двойного неравенства:

; .

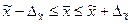
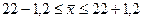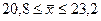Таким образом, с вероятностью 0,954 можно утверждать, что средняя продолжительность расчетов предприятий данной корпо­рации колеблется в пределах от 20,8 до 23,2 дней.

Задача 2. Среди выборочно обследованных 1000 семей региона по уровню душевого дохода (выборка 2%-ная, механическая) мало­обеспеченных оказалось 300 семей.

Требуется с вероятностью 0,997 определить долю мало­обеспеченных семей во всем регионе.

Решение. Выборочная доля (доля малообеспеченных семей сре­ди обследованных семей) равна:

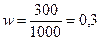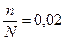; или 2% (по условию).

По представленным ранее данным Ф(t) для вероятности 0,997 находим t = 3 (см. п. 6.3). Предельную ошибку доли определя­ем по формуле бесповторного отбора (механическая выборка всегда является бесповторной):

.

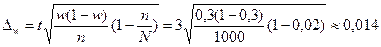Предельная относительная ошибка выборки, %:

.

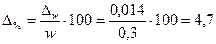Генеральная доля р = w ± ∆_w, а доверительные пределы гене­ральной доли исчисляем, исходя из двойного неравенства: w-∆_w≤p≤w +∆ _w.

В нашем примере:

0,3-0,014≤ p≤ 0,3+0,014;

0,286≤ p≤ 0,314 или 28,6%≤ p≤ 31,4%

Таким образом, почти достоверно, с вероятностью 0,997 можно утверждать, что доля малообеспеченных семей среди всех семей региона колеблется от 28,6 до 31,4%.

Задача 3. Для определения урожайности зерновых культур про­ведено выборочное обследование 100 хозяйств региона различных форм собственности, в результате которого получены сводные дан­ные (табл.6.1). Необходимо с вероятностью 0,954 опреде­лить предельную ошибку выборочной средней и доверительные пределы средней урожайности зерновых культур по всем хозяйст­вам региона.

Таблица 6.1

Дата добавления: 2014-01-06