Решение. Среднемесячная заработная плата и число работников м п/п Отрасль экономики Заработная плата

Среднемесячная заработная плата и число работников

м п/п	Отрасль экономики	Заработная плата, руб.	Число работников, чел.
		Январь	Сентябрь	Январь	Сентябрь
		X0	X1	То	Т1
1. 2. 3.	Здравоохранение Образование Культура и искусство

Исчислить: индекс заработной платы переменного соста­ва, постоянного состава и структурных сдвигов.

1. Для исчисления индекса заработной платы переменного состава вначале определим среднюю заработную плату в январе и сентябре ме­сяцах. Обозначим заработную плату через х, а число работников — Т.

► Январь:

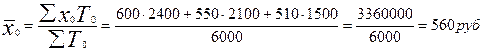
►Сентябрь:

2. Теперь исчислим индекс заработной платы переменного состава:

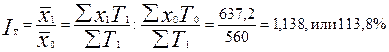
Следовательно, средняя заработная плата работников по данным трем отраслям экономики в сентябре по сравнению с январем выросла на 13,8%.

Абсолютный прирост средней заработной платы составил

637,2 - 560 = 77,2 руб.

Изменение средней заработной платы происходило под влиянием двух факторов: изменения уровня заработной платы в каждой отрасли экономики и изменения структуры численности работников.

3. Исчислим индекс заработной платы постоянного состава:

Следовательно, средняя заработная плата работников по данным от­раслям экономики в сентябре по сравнению с январем выросла на 14,9% в результате изменения только одного фактора — самой заработной пла­ты по каждой отрасли экономики (без учета структурных изменений в численности работников).

Абсолютный прирост средней заработной платы составил 637,2 — 554,8 = 82,4 руб.

4. Вычислим влияние изменения структуры численности работни­ков на динамику средней заработной платы на основе индекса структурных сдвигов:

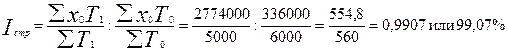
Следовательно, увеличение доли работников с меньшей заработной платой в общей их численности привело к снижению средней заработ­ной платы по трем отраслям вместе на 0,03%, хотя в каждой отрасли в отдельности она возросла.

Абсолютное снижение средней заработной платы составило 554,8 — 560 = - 5,2 руб., что совпадает с разностью исчисленных выше прирос­тов заработной платы: 77,2 — 82,4 = — 5,2 руб.

Отрицательный эффект структурных сдвигов объясняется тем, что в сентябре по сравнению с январем в большей мере сократилась доля ра­ботников с наиболее высоким уровнем заработной платы, т.е. в здраво­охранении (с 40 до 32%).

8.5. Базисные и цепные индексы

Часто в ходе экономического анализа изменение индекси­руемых величин изучают не за два, а за ряд последовательных периодов. Следовательно, возникает необходимость построения индексов за ряд этих последовательных периодов, которые обра­зуют индексные системы. Такие системы характеризуют изме­нения, происходящие в изучаемом явлении в течение исследуе­мого периода времени.

В зависимости от базы сравнения индексы бы­вают базисными и цепными.

В системе базисных индексов сравнения уровней индексируе­мого показателя в каждом индексе производится с уровнем базис­ного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.

Цепные и базисные индексы могут быть как индивидуаль­ные, так и общие.

Ряды индивидуальных индексов просты по построению. Так, например, обозначив четыре последовательных периода под­строчными значениями 0, 1, 2, 3, исчисляем базисные и цепные индивидуальные индексы цен:

· базисные индексы: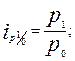

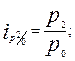
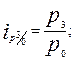
· цепные индексы: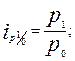

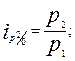
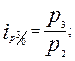
Между цепными и базисными индивидуальными индексами существует взаимосвязь, позволяющая переходить от одних ин­дексов к другим — произведение последовательных цепных индиви­дуальных индексов дает базисный индекс последнего периода:

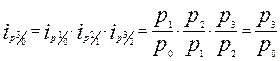
Отношение базисного индекса отчетного периода к базисно­му индексу предшествующего периода дает цепной индекс от­четного периода:

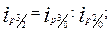
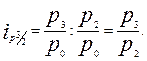
Это правило позволяет применять так называемый цепной метод, т.е. находить неизвестный ряд базисных индексов по из­вестным цепным и наоборот.

Рассмотрим возможность применения цеп­ного метода исчисления для агрегатных индексов.

Как известно, в каждом отдельном индексе веса в его чис­лителе и знаменателе обязательно фиксируются на одном и том же уровне.

Если же строится ряд индексов, то веса в нем могут быть либо постоянными для всех индексов ряда, либо переменными.

Рассмотрим построение базисных и цепных индексов на при­мере агрегатных индексов цен и физического объема продукции.

► Базисные индексы:

● индексы цен Пааше (с переменными весами):

…;

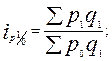
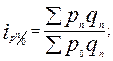
● индексы цен Ласпейреса (с постоянными весами):

…

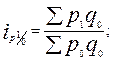
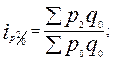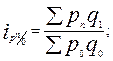
● индексы физического объема продукции (с постоянными весами):

…

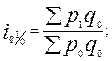
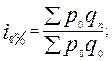
► Цепне индексы:

● индексы цен Паше( с переменными весами ):

…

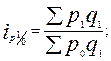
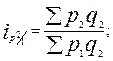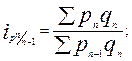
● индексы цен Лайспереса( с постоянными весами ):

…

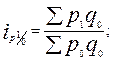
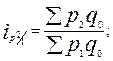● индексы физического объема продукции (с постоянными весами):

…

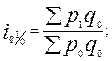
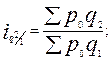Итак, в базисных агрегатных индексах все отчетные данные сопоставляются только с базисными (закрепленными) данными, а в цепных — с предыдущими (в данном случае - смежными) данными.

Период весов во всех индексах цен Пааше взят текущий (индексы с переменными весами), в индексах физического объема и индексах цен Ласпейреса — закрепленный (индексы с постоянными весами).

Постоянные веса (не меняющиеся при переходе от одного индекса к другому) позволяют исключить влияние изменения структуры на значение индекса.

Ряды агрегатных индексов с постоянными весами имеют преимущество — сохраняется взаимосвязь между цепными и базисными индексами, например, в ряду агрегатных индексов физического объема:

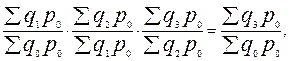
или в ряду агрегатных индексов цен Ласпейреса:

Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных общих индексов к базисными наоборот.

В рядах агрегатных индексов качественных показателей, которые строятся с переменными весами (например, ряд цен Пааше), перемножение цепных индексов не дает базисный:

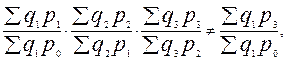
Для таких индексов переход от цепных индексов к базисным (и наоборот) невозможен. Вместе стем, встатистической практике часто возникает необходимость определения динамики цен за дли­тельный период времени на основе цепных индексов цен с пере­менными весами. Тогда для получения приближенного базисного (итогового) индекса цепные индексы цен перемножают, заведомо зная, что втаком расчете допускается ошибка. Отдельные индексы этого ряда используются для пересчета стоимостных показателей отчетного периода в ценах предыдущего года. Основные формулы для расчета общих индексов приведены в табл. 8.6.

Таблица 8.6

Дата добавления: 2014-01-06