Решение. Количество себестоимость произведенной продукции Фирма Произведено мужской обуви, тыс

Количество себестоимость произведенной продукции

Фирма	Произведено мужской обуви, тыс. пар	Себестоимость единицы продукции, руб.
	Базисный период	Базисный период	Базисный период	Отчетный период
	q0	q1	z0	z1
«Олимп» «Омега»

Исчислить: изменение общих затрат на производство всей продукции под совместным влиянием двух факторов - изменения физического объема продукции и цен каждого из этих факторов в отдельности.

1. Для проведения факторного анализа воспользуемся индекс­ной системой:

откуда

1. Совокупное действие двух факторов на изменение общих за­трат определим с помощью индекса затрат на производство продук­ции (результативного индекса):

или 116,7%

Индекс показывает, что затраты на производство всей продук­ции в отчетном периоде по сравнению с базисным увеличились на 16,7%, что в абсолютном выражении составило:

Δzq=∑ z₁ q₁ -∑ z₀ q₀ = 6300-5400 = 90

3. Влияние изменения себестоимости единицы продукции на величину общих затрат определим с помощью факторного индекса себестоимости продукции:

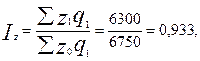или 93,3%

Следовательно, за счет изменения себестоимости единицы про­дукции по каждой фирме произошло снижение общих затрат на производство продукции на 6,7%, что в абсолютном выражении со­ставило:

4. Влияние изменения объема продукции на величину общих затрат определим с помощью факторного индекса физического объема продукции:

или 125,0%

Следовательно, за счет роста общего объема произведенной про­дукции затраты на производство всей продукции выросли на 25%, что в абсолютном выражении составило:

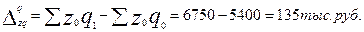
Проверим взаимосвязь индексов и разложение абсолютного прироста по факторам.

Izq=Iz ∙ Iq; 1,167 = 1,25 ∙ 0,933; 1,167 = 1,167;

; 90 = -45 + 135;. 90 = 90.

Контрольные вопросы

1. Что называется индексом в статистике?

2. Какие задачи решают при помощи индексов?

3. Что характеризуют индивидуальные индексы? Приведите примеры.

4. В чем сущность общих индексов?

5. Для чего необходимо деление на индексы объемных (количественных) и качественных показателей и какая система взвеши­вания принята в теории индексов?

6. Как исчисляется агрегатный индекс стоимости продукции (то­варооборота в фактических ценах) и что он характеризует?

7. Как исчисляется агрегатный индекс физического объема про­дукции (товарооборота) и что он характеризует? Напишите формулу.

8. Когда возникает необходимость преобразования индекса физи­ческого объема в средний арифметический и средний гармони­ческий; каким образом происходят такие преобразования? По­кажите на примерах.

9. Как исчисляют агрегатные индексы цен (Пааше и Ласпейреса), себестоимости, производительности труда и что они показы­вают? Напишите их формулы.

10. Когда возникает необходимость преобразования агрегатного индекса цен в средний гармонический и средний арифметиче­ский, каким образом происходят такие преобразования? По­кажите на примере.

11. Какой вариант агрегатных индексов качественных показателей используют при расчете индекса потребительских цен и почему?

12. Что называется индексом переменного состава, как он исчис­ляется и что характеризует? Напишите его формулу.

13. Какой индекс называется индексом постоянного состава, как он исчисляется и что характеризует?

14. Что характеризует индекс структурных сдвигов и как он исчисляется?

15. Какая взаимосвязь существует между индексами переменного, постоянного состава и структурных сдвигов?

16. Как строятся базисные и цепные индексы и какая между ними существует взаимосвязь?

17. Что представляют собой индексы с постоянными и переменными весами?

18. Что представляет собой система взаимосвязанных индексов, для чего она применяется?

19. В чем выражается взаимосвязь индексов цен, физического объ­ема и товарооборота, как практически она используется?

20. Какая система взаимосвязанных индексов используется при анализе себестоимости, физического объема и затрат в производстве?

21. Как определить долю влияния различных факторов на изменение результативного показателя?

22. В каких случаях производится разложение индексов по трем и бо­лее факторам?

23. Как осуществляется разложение абсолютного прироста по фак­торам? Что оно характеризует?

Глава 9. Статистические методы изучения взаимосвязи социально-экономических явлений

9.1. Стохастико-детерминированный характер социально-экономических явлений и виды связей между ними

Наука исходит из объективной закономерной взаимосвязи и причинной обусловленности всех явлений.

Изучение статистических закономерностей — важнейшая по­знавательная задача статистики, которую она решает с помощью особых методов, видоизменяющихся в зависимости от характера исходной информации и целей познания. Знание характера и силы связей позволяет управлять социально-экономическими процесса­ми и предсказывать их развитие. Особую актуальность это приоб­ретает в условиях развивающейся рыночной экономики. Изучение механизма рыночных связей, взаимодействия спроса и предложе­ния, влияния объема и структуры товарооборота на объем и состав производства продукции, формирования товарных запасов, издер­жек производства, прибыли и других качественных показателей имеет первостепенное значение для прогнозирования конъюнкту­ры рынка, региональной организации производственных и торго­вых процессов, успешного ведения бизнеса.

Среди многих форм связей важнейшей является причинная, определяющая все другие формы. Сущность причинности со­стоит в порождении одного явления другим. Вместе с тем, при­чина сама по себе еще не определяет следствия, она зависит также от условий, в которых протекает действие причины. Для возникновения следствия нужны все определяющие его факто­ры — причина и условия. Необходимая обусловленность явле­ний множеством факторов называется детерминизмом.

Объектами исследования при статистическом измерении связей служит, как правило, детерминированность следствия факторами (причиной и условиями). Признак, характеризую­щий следствие, называется результативным; признаки, харак­теризующие причины, — факторными. Выявление связей ме­жду признаками основывается на результатах качественного теоретического анализа. Задача статистики — количественная оценка закономерности связей, математическая определен­ность позволяет использовать результаты экономических разработок для практических целей. Вместе с тем, качественный анализ должен не только предшествовать статистическому, но и являться подтверждением справедливости его результатов.

Связи между явлениями и их признаками классифицируют по степени тесноты связи, направлению и аналитическому вы­ражению.

9.1.1. Функциональные

и стохастическue связи

Между различными явлениями и их признаками необходимо прежде всего выделить два типа связей: функциональную (же­стко детерминированную) и статистическую (стохастически де­терминированную).

В соответствии с жестко детерминистическим представлением о функционировании экономических систем необходимость и закономерность однозначно проявляются в каждом отдельном явлении, т. е. любое действие вызывает строго определенный ре­зультат; случайными (непредвиденными заранее) воздействиями при этом пренебрегают. Поэтому при заданных начальных усло­виях состояние такой системы может быть определено с вероят­ностью, равной единице. Разновидностью такой закономерности является функциональная связь.

Связь признака у с признаком x называется функциональ­ной, если каждому возможному значению независимого призна­ка х соответствует одно или несколько строго определенных значений зависимого признака у. Определение функциональ­ной связи может быть легко обобщено для случая многих при­знаков х₁, х_2,...,х_п.

Характерной особенностью функциональных связей является то, что в каждом отдельном случае известен полный перечень факторов, определяющих значение зависимого (результативно­го) признака, а также точный механизм их влияния, выражен­ный определенным уравнением.

Функциональную связь можно представить уравнением:

где y_i — результативный признак (i = 1,...,n);

f(Xi) — известная функция связи результативного и факторного при­знаков;

x_i — факторный признак.

Чаще всего функциональные связи наблюдаются в явлениях, описываемых математикой, физикой и другими точными науками. Имеют место функциональные связи и в социально-экономических процессах, но довольно редко (они отражают взаимосвязь только отдельных сторон сложных явлений общественной жизни). В экономике примером функциональной связи может служить связь между оплатой труда у и количеством изготовленных деталей x при простой сдельной оплате труда. Так, если расценка за одну деталь составляет 3 тыс. руб., то связь между признаками однозначно выразится простым линейным уравнением у = 3х. Для каждого допустимого значения х можно указать вполне определенное значени­е у.

Если, положим, х = 5, то соответственно у =15.

В реальной общественной жизни, ввиду неполноты информации жестко детерминированной системы, может возникнуть неопределенность, из-за которой эта система по своей природе должна рассматриваться как вероятностная, при этом связь между признаками становится стохастической.

Стохастическая связь — это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величин х₁, х_2,...,х_п (случайных или неслучайных) изменением закона распределения. Это обусловливается тем, что зависимая переменная (результативный признак), кроме рассматриваемых независимых, подвержена влиянию ряда неучтенных или неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибок измерения переменных. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.

Характерной особенностью стохастических связей является то, что они проявляются во всей совокупности, а не в каждой ее единице (причем не известен ни полный перечень факторов, определяющих значение результативного признака, ни точный механизм их функционирования и взаимодействия с результативным признаком). Всегда имеет место влияние случайного. Появляющиеся различные значения зависимой переменной — реализации случайной величины.

Модель стохастической связи может быть представлена в общем виде уравнением:

(9.1)

где — расчетное значение результативного признака;

f(x_i) — часть результативного признака, сформировавшаяся под воз-

действием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком;

ε_i — часть результативного признака, возникшая вследствие

действия неконтролируемых или неучтенных факторов, а также измерения признаков, неизбежно сопровождающегося некоторыми случайными ошибками.

Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет сущест­венную силу, проявится достаточно отчетливо.

В социально-экономической жизни приходится сталкиваться со многими явлениями, имеющими вероятностный характер. Например, уровень производительности труда рабочих стохасти­чески связан с целым комплексом факторов: квалификацией, стажем работы, уровнем механизации и автоматизации произ­водства, интенсивностью труда, простоями, состоянием здоро­вья работника, его настроением, атмосферным давлением и др. Полный перечень факторов неизвестен. Кроме того, неодинаково действие любого известного фактора на уровень производительности труда каждого рабочего. Изменение атмосферно: давления, к примеру, значительно снижает работоспособность рабочих, страдающих заболеваниями сердечно-сосудистой системы, и практически не сказывается на производительности труда здоровых. В результате — при одинаковых возможностях наблюдается распределение значений дневной выработки рабочих. Такое распределение носит условный характер, поскольку оно связано с фиксированными значениями факторных признаков. Различия условных распределений имеют выраженную направ­ленность связи (например, выработка растет с повышением ква­лификации рабочего). Эту направленность связи можно рас­крыть более наглядно, если ограничиться рассмотрением только одного аспекта стохастической связи — изучением вместо ус­ловных распределений лишь одного их параметра — условного математического ожидания (частные случаи стохастической свя­зи — корреляционная и регрессионная).

Корреляционнаясвязь существует там, где взаимосвязанные явления характеризуются только случайными величинами. При такой связи среднее значение (математическое ожидание) случайной величины результативного признака у закономерно изменяется в зависимости от изменения другой величины x или других случайных величин х₁, х_2,...,х_п. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом. Только при достаточно большом количестве случаев каждому значению случайного признака х будет соответствовать распределение средних значений случайного признака y. Наличие корреляционных связей присуще многим общественным явлениям.

Известно, что увеличение количества внесенных удобрений ведет к повышению урожайности. Это справедливое положение, подтверждаемое в массе явлений, совсем не означает, что на от­дельных одинаково удобренных участках будет одинаковая уро­жайность одной и той же сельскохозяйственной культуры. Веро­ятнее всего, уровни урожайности будут различаться. Кроме того, существует вероятность, что более высокая урожайность может наблюдаться на менее удобренных участках: на урожайность влияет не только количество внесенных в почву удобрений, но и другие, неучтенные факторы (качество семян, предшествующие культуры, рельеф местности, агротехника земледелия, сроки и качество посева и уборки). Но если в анализ включить достаточ­но большое число площадей, то обнаружится прямая корреляционная зависимость между количеством внесенных удобрений (в допустимых пределах) и средним уровнем урожайности. Значит, важная особенность корреляционных связей (как и других стохастических) состоит в том, что они обнаруживаются не в еди­ничных случаях, а в массовых явлениях и требуют для своего ис­следования массовых наблюдений, т. е. статистических данных.

Корреляционная связь — понятие более узкое, чем стохасти­ческая связь. Последняя может отражаться не только в измене­нии средней величины, но и в вариации одного признака в за­висимости от другого, т. е. любой другой характеристики вариа­ции. Таким образом, корреляционная связь, является частным случаем стохастической связи.

► Прямые и обратные связи. В зависимости от направления действия функциональные и стохастические связи могут быть прямыми и обратными. При прямой связи направление измене­ния результативного признака совпадает с направлением изме­нения признака-фактора, т. е. с увеличением факторного при­знака увеличивается и результативный, и наоборот, с уменьше­нием факторного признака уменьшается и результативный при­знак. В противном случае между рассматриваемыми величинами существуют обратные связи. Например, чем выше квалифика­ция рабочего (разряд), тем выше уровень производительности труда — прямая связь. А чем выше производительность труда, тем ниже себестоимость единицы продукции — обратная связь.

► Прямолинейные и криволинейные связи. По аналитическо­му выражению (форме) связи могут быть прямолинейными и криволинейными. При прямолинейной связи с возрастанием значения факторного признака происходит непрерывное возрас­тание (или убывание) значений результативного признака. Математически такая связь представляется уравнением прямой, а графически — прямой линией. Отсюда ее более короткое название — линейная связь.

При криволинейных связях с возрастанием значения фак­торного признака возрастание (или убывание) результатив­ного признака происходит неравномерно или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, пара­болой и т.д.).

► Однофакторные и многофакторные связи. Поколичеству факторов, действующих на результативный признак, связи раз­личаются однофакторные (один фактор) и многофакторные (два и более факторов). Однофакторные (простые) связи обыч­но называются парными (так как рассматривается пара призна­ков). Например, корреляционная связь между прибылью и производительностью труда. В случае многофакторной (множе­ственной) связи имеют в виду, что все факторы действуют комплексно, т.е. одновременно и во взаимосвязи, например, корреляционная связь между производительностью труда и уровнем организации труда, автоматизации производства, ква­лификации рабочих, производственным стажем, простоями и другими факторными признаками.

С помощью множественной корреляции можно охватить весь комплекс факторных признаков и объективно отразить су­ществующие множественные связи.

9.2. Статистические методы моделирования связи

Для изучения функциональных связей применяются балансо­вый и индексный методы.

Для исследования стохастических связей широко использу­ется метод сопоставления двух параллельных рядов, метод анали­тических группировок, корреляционный анализ, регрессионный ана­лиз и некоторые непараметрические методы.

9.2.1. Простейшие методы изучения стохастических связей

► Метод сопоставления двух параллельных рядов. Устано­вить наличие стохастической связи, а также получить пред­ставление о ее характере и направлении можно с помощью со­поставления двух параллельных рядов статистических величин. Для этого факторы, характеризующие результативный признак, располагают в возрастающем или убывающем порядке (в зависимости от эволюции процесса и целей исследования), а затем прослеживают изменение величины результативного признака. Сопоставление и анализ расположенных таким образом рядов значений изучаемых величин позволяют установить наличие связи и ее направление. Зависимость между факторами и показателями может прослеживаться во времени (параллельные динамические ряды).

До исследования методом параллельных рядов (априори) необходимо провести анализ сопоставляемых явлений и установить наличие между ними причинных связей (а не простого сопутствия). Например, только потому, что между урожайностью и себестоимостью продукции сельского хозяйства имеется причинная связь, становится возможным построение, а затем сопоставление параллельных рядов этих показателей.

К недостатку метода взаимозависимых параллельных рядов следует отнести невозможность определения количественной меры связи между изучаемыми признаками. Однако он удобен и эффективен, когда речь идет о необходимости установления связей между показателями и факторами, характеризующими экономический процесс.

► Метод аналитических группировок. Стохастическая связь будет проявляться отчетливее, если применить для ее изучения аналитические группировки. Чтобы выявить зависимость с помо­щью этого метода, нужно произвести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака. Сопоставляя затем изменения результативного признака по мере изменения факторного, можно выявить направление, характер и тесноту связи между ними с помощью эмпирического корреляционного отношения (см. в главах 5.3 и 9.2.2.3). Однако метод группировок не позволяет определить форму (аналитическое выражение) влияния факторных признаков на результативный.

9.2.2. Статистическое моделирование связи методом корреляционного и регрессионного

анализа

В общем виде задача статистики в области изучения взаимо­связей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.

Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых, должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на резуль­тативный признак.

Задачи регрессионного анализа — выбор типа модели (формы связи), установление степени влияния независимых перемен­ных на зависимую и определение расчетных значений зависи­мой переменной (функции регрессии).

Решение всех названных задач приводит к необходимости комплексного использования этих методов.

9.2.2.1 Корреляционный и регрессионный анализ

Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле модель — это аналог, условный образ (изображение, описание, схема, чертеж и т.п.) какого-либо объекта, процес­са или события, приближенно воссоздающий «оригинал». Модель представляет собой логическое или математическое описание компонентов и функций, отображающих сущест­венные свойства моделируемого объекта или процесса, дает возможность установить основные закономерности изменения оригинала. В модели оперируют показателями, исчисленными для качественно однородных массовых явлений (совокупно­стей). Выражение модели в виде функциональных уравнений используют для расчета средних значений моделируемого по­казателя по набору заданных величин и для выявления степе­ни влияния на него отдельных факторов.

По количеству включаемых факторов модели могут быть однофакторными и многофакторными (два и более факторов).

В зависимости от познавательной цели стати­стические модели подразделяются на структурные, динамические и модели связи.

Рассмотрим основные проблемы статистического моделирования связи методами корреляционного и регрессионного анализа.

9.2.2.2. Двухмерная линейная модель

корреляционного и регрессионного анализа

(однофакторный линейный корреляционный

и регрессионный анализ)

Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака x: на результативный признак y и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей.

Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции т опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически — перебором и оценкой функций разных типов и т.п.

При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной корреляционной связи имеет вид:

(9.2)

де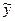 — теоретические значения результативного признака, полу­ченные по уравнению регрессии;

a_0, a₁ — коэффициенты (параметры) уравнения регрессии.

Поскольку a₀ является средним значением у в точке х = 0,

экономическая интерпретация часто затруднена или вообще

невозможна.

Коэффициент парной линейной регрессии а₁ имеет смысл

показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Уравнение (9.2) показывает среднее значение изменения результативного признака y при изменении факторного признака х на одну единицу его из­мерения, т. е. вариацию у, приходящуюся на единицу вариации х. Знак a₁ указывает направление этого изменения.

Параметры уравнения a_0, a₁ находят методом наименьших квадратов (метод решения систем уравнений, при котором в ка­честве решения принимается точка минимума суммы квадратов отклонений), т. е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических дан­ных y_i от выровненных :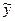

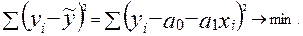
Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

(9.3)

Решим эту систему в общем виде:

Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:

или

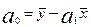
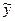Определив значения a₀ , a₁ и подставив их в уравнение свя­зи , находим значения , зависящие только от за­данного значения х.

Пример 1. Рассмотрим построение однофакторного уравнения рег­рессии зависимости производительности труда у от стажа работы х по данным табл. 9.1 (10 рабочих одной бригады заняты производством ра­диоэлектронных изделий, данные ранжированы по стажу их работы).

Исходя из экономических соображений стаж работы выбран в качест­ве независимой переменной х. Сопоставление данных параллельных ря­дов признаков х и у (табл. 9.1) показывает, что с возрастанием признака X (стажа работы), растет, хотя и не всегда, результативный признак у (производительность труда). Следовательно, между х и у существует пря­мая зависимость, пусть неполная, но выраженная достаточно ясно.

Таблица 9.1

Дата добавления: 2014-01-06