
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределение рабочих бригады по выработке и стажу работы
|
|
|
|
| Исходные данные | Расчетные значения | |||||
| Номер рабочего | Стаж работы, годы X | Дневная выработка рабочего, шт. У | 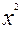
| 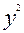
| ху | 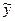
|
| 4-й | 4,6 | |||||
| 6-й | 5,2 | |||||
| 3-й | 5,8 | |||||
| 1-й | 6,4 | |||||
| 2-й | 7,0 | |||||
| 7-й | 7,6 | |||||
| 9-й | 8,2 | |||||
| 10-й | 8,8 | |||||
| 8-й | 9,4 | |||||
| 5-й | 10,0 | |||||
| Итого | ∑x=55 | ∑y = 73 | ∑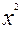 = 385 = 385
| ∑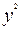 = 565 = 565
| ∑xy= 451 | 73,0 |
Для уточнения формы связи между рассматриваемыми признаками используем графический метод. Нанесем на график точки, соответствующие значениям х, у, получим корреляционное поле, а соединив их отрезками, — ломаную регрессии (рис. 9.1).
Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис.,9.1), которая может быть выражена простым линейным уравнением регрессии:
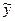 = a0 + a1 х,
= a0 + a1 х,
где 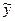 — теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии;
— теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии;
a0, a1, - неизвестные параметры уравнения регрессии;
х - стаж работы рабочих, годы.
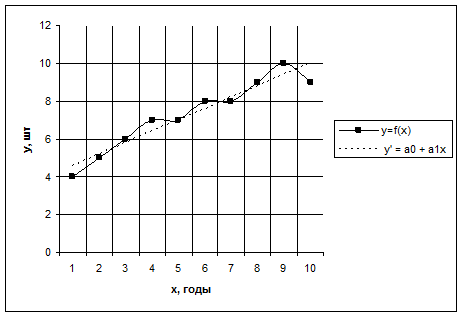
Рис.9.1. Зависимость выработки одного рабочего
от стажа работы х (по данным табл. 9.1)
Пользуясь расчетными значениями (см. табл. 9.1), исчислим параметры для данного уравнения регрессии:
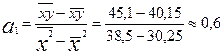
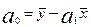 = 7,3-0,6 ∙ 5,5 = 4,0.
= 7,3-0,6 ∙ 5,5 = 4,0.
Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного простого уравнения регрессии:
|
|
|
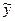 =4,0+0,6x
=4,0+0,6x
Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значения 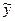 , найденные по данному уравнению, приведены в табл. 9.1. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм ∑y = ∑
, найденные по данному уравнению, приведены в табл. 9.1. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм ∑y = ∑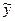 (при этом возможно некоторое расхождение вследствие округления расчетов).
(при этом возможно некоторое расхождение вследствие округления расчетов).
9.2.2.3 Проверка адекватности
регрессионной модели
Для практического использования моделей регрессии очень важна их адекватность,
т. е. соответствие фактическим статистическим данным.
Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции — параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей.
При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин.
Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n< 30) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t- критерия:
для параметра a0
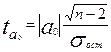 (9.4)
(9.4)
для параметра a1
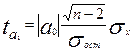 (9.5)
(9.5)
где n – объем выборки;
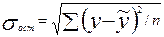 – среднее квадратическое отклонение результативного признака y от выравненных значений
– среднее квадратическое отклонение результативного признака y от выравненных значений 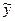 ;
;
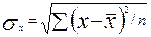 или
или 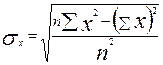 – среднее квадратическое отклонение факторного признака x от общей средней
– среднее квадратическое отклонение факторного признака x от общей средней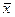 .
.
|
|
|
Вычисленные по формулам (9.4) и (9.5) значения, сравнивают с критическими t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости α и числом степеней свободы вариации ν = n - 2. В социально-экономических исследованиях уровень значимости α обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если tрасч > tтабл. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. Для проверки значимости коэффициентов регрессии исследуемого уравнения 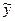 = 4,0 + 0,6х исчислим t-критерий Стьюдента с ν = 10 — 2 = 8 степенями свободы. Рассмотрим вспомогательную таблицу (табл. 9.2).
= 4,0 + 0,6х исчислим t-критерий Стьюдента с ν = 10 — 2 = 8 степенями свободы. Рассмотрим вспомогательную таблицу (табл. 9.2).
Таблица 9.2
Расчетные значения, необходимые для исчисления дост, дx
у-
| (у- )2 )2
| 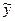 - -
| (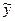 - - )2 )2
| y-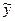
| 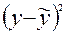
|
| -3,3 | 10,89 | -2,7 | 7,29 | -0,6 | 0,36 |
| -2,3 | 5,29 | -2,1 | 4,41 | -0,2 | 0,04 |
| -1,3 | 1,69 | -1,5 | 2,25 | 0,2 | 0,04 |
| -0,3 | 0,09 | -0,9 | 0,81 | 0,6 | 0,36 |
| -0,3 | 0,09 | -0,3 | 0,09 | 0,0 | 0,0 |
| 0,7 | 0,49 | 0,3 | 0,09 | 0,4 | 0,16 |
| 0,7 | 0,49 | 0,9 | 0,81 | -0,2 | 0,04 |
| 1,7 | 2,89 | 1,5 | 2,25 | 0,2 | 0,04 |
| 2,7 | 7,29 | 2,1 | 4,41 | 0,6 | 0,36 |
| 1,7 | 2,89 | 2,7 | 7,29 | -1,0 | 1,0 |
| Итого | 32,10 | — | 29,70 | — | 2,40 |
Средние квадратические отклонения (см. табл. 9.1):
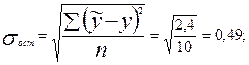
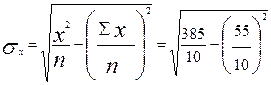 =2,87.
=2,87.
Расчетные значения t- критерия Стьюдента:
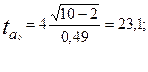

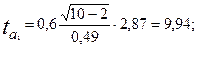
По таблице распределения Стьюдента для ν= 8 находим критическое значение t-критерия: (tтабл = 3,307 при α = 0,05).
Поскольку расчетное значение tрасч > tтабл, оба параметра a0, a1 признаются значимыми (отклоняется гипотеза о том, что каждый из этих параметров в действительности равен нулю, и лишь в силу случайных обстоятельств оказался равным проверяемой величине).
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у. Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционнымотношением ηэ, когда 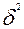 (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней: ηэ =
(межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней: ηэ =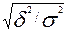 .
.
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения — теоретическое.
Теоретическое корреляционное отношение η представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значений результативного признака δ, т. е. рассчитанных по уравнению регрессии, со средним квадратическим отклонением эмпирических (фактических) значений результативного признака σ:
|
|
|
ηэ =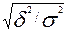 .
.
Где 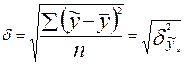 ;
; 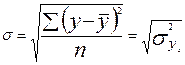
Тогда η=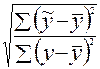 (9.6)
(9.6)
Изменение значения η объясняется влиянием факторного признака.
В основе расчета корреляционного отношения лежит правило
сложения дисперсий (см. главу 5), т. е.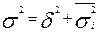 , где
, где 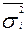 - отражает вариацию у за счет всех остальных факторов, кроме х, т. е. является остаточной дисперсией:
- отражает вариацию у за счет всех остальных факторов, кроме х, т. е. является остаточной дисперсией:
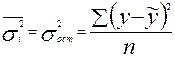
Тогда формула теоретического корреляционного отношения примет вид:
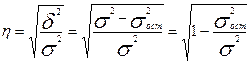 (9.7)
(9.7)
или 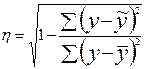 (9.8)
(9.8)
Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации (меры определенности, причинности). Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора.
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком. При криволинейных связях теоретическое корреляционное отношение, исчисляемое по формулам (9.7), (9.8), часто называют индексом корреляции R. При значительной корреляции расчет по формулам (9.7) и (9.8) значительно проще, так как отклонение (у-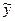 ), как правило, по значению меньше, чем отклонение (
), как правило, по значению меньше, чем отклонение (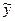 -
- ).
).
Как видно из формул (9.7) и (9.8), корреляционное отношение может находиться в пределах от 0 до 1, т. е. (0 ≤ η ≤ 1). Чем ближе корреляционное отношение к 1, тем связь между признаками теснее.
Проиллюстрируем расчет теоретического корреляционного отношения как меры тесноты связи на примере, рассмотренном в табл.9.1, для которого по уравнению прямой регрессии 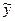 = 4 + 0,6x найдены значения дневной выработки каждого рабочего.
= 4 + 0,6x найдены значения дневной выработки каждого рабочего.
Теоретическое корреляционное отношение рассчитываем двумя способами (см. данные табл.9.2):
По формуле (9.6) 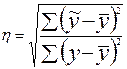 =
=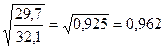 ;
;
По формуле (9.8) 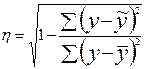 =
=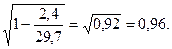
|
|
|
Полученное значение теоретического корреляционного отношения свидетельствует о возможном наличии весьма тесной прямой зависимости между рассматриваемыми признаками.
Коэффициент детерминации равен 0,925. Отсюда заключаем, что 92,5% общей вариации выработки в изучаемой бригаде обусловлено вариацией фактора — стажа работы рабочих (и только 7,5% общей вариации нельзя объяснить изменением стажа работы).
Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - линейный коэффициент корреляции:
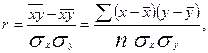 (9.9)
(9.9)
где n— число наблюдений.
Для практических вычислений при малом числе наблюдений, n ≤ (20 ÷30), линейный коэффициент корреляции удобнее исчислять по следующей формуле:
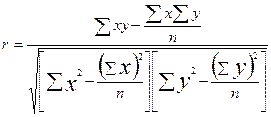 . (9.10)
. (9.10)
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1 ≤ r ≤ +1.
Отрицательные значения указывают на обратную связь, положительные — на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при r= ±1 связь — функциональная.
Используем данные табл. 9.1 и рассчитаем линейный коэффициент корреляции по формуле (9.10):
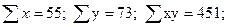
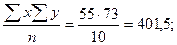
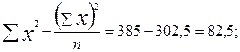
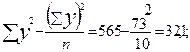
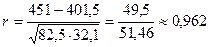
Квадрат линейного коэффициента корреляции 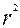 называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т. е. 0 <
называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т. е. 0 < 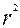 < 1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
< 1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
Факт совпадений и несовпадений значений теоретического корреляционного отношения з и линейного коэффициента корреляции r используется для оценки формы связи.
Выше отмечалось, что посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции - только прямолинейной. Следовательно, значения η и r совпадают только при наличии прямолинейной связи. Несовпадение этих значений свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов 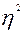 и
и 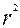 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной. В приведенном ранее примере совпадение значений η и r (η = r = 0,962) дает основание считать связь между выработкой рабочих и их стажем прямолинейной.
не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной. В приведенном ранее примере совпадение значений η и r (η = r = 0,962) дает основание считать связь между выработкой рабочих и их стажем прямолинейной.
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.
Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.
При линейной однофакторной связи t-критерий можно рассчитать по формуле:
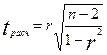 (9.11)
(9.11)
где (n -2) — число степеней свободы при заданном уровне значимости б и объеме выборки п.
Полученное значение tрасч сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение tрасч превосходит табличное значение критерия tтабл, то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т. е. отклоняется гипотеза о его случайности).
Так, для коэффициента корреляции между выработкой и стажем работы получим:
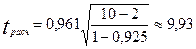
Это значительно больше критического значения t для n — 2 = 8 степеней свободы и α = 0,01 (tтабл = 3,356), что свидетельствует о значимости коэффициента корреляции и существенности связи между выработкой и стажем работы.
Таким образом, построенная регрессионная модель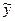 = 4 + 0,6x в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю гипотетическую генеральную совокупность.
= 4 + 0,6x в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю гипотетическую генеральную совокупность.
9.2.2.4. Экономическая интерпретация параметров регрессии
После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель).
В рассмотренном уравнении 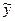 =4+0,6x, характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр a1 >0. Следовательно, с возрастанием стажа выработка, как и ожидалось, также увеличивается.
=4+0,6x, характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр a1 >0. Следовательно, с возрастанием стажа выработка, как и ожидалось, также увеличивается.
Из уравнения следует, что возрастание на 1 год стажа рабочего приводит к увеличению им дневной выработки в среднем на 0,6 изделия (величину параметра a1).
Для удобства интерпретации параметра a1используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %:
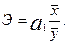 (9.12)
(9.12)
В рассматриваемом примере Э = 0,6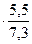 = 0,45. Следовательно, с возрастанием стажа работы на 1 % следует ожидать повышения производительности труда в среднем на 0,45 %.
= 0,45. Следовательно, с возрастанием стажа работы на 1 % следует ожидать повышения производительности труда в среднем на 0,45 %.
Этот вывод справедлив только для изучаемой совокупности рабочих при конкретных условиях работы.
Если данная совокупность и условия работы типичны, то коэффициент регрессии может быть использован для нормирования и планирования производительности труда рабочих этой профессии.
Имеет смысл вычислить остатки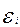 =у -
=у - 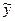 , характеризующие отклонение i -х наблюдений от значений, которые следует ожидать в среднем.
, характеризующие отклонение i -х наблюдений от значений, которые следует ожидать в среднем.
Анализируя остатки, можно сделать ряд практических выводов. Значения остатков (см. табл.9.2) имеют как положительные, так и отрицательные отклонения от ожидаемого уровня анализируемого показателя. Экономический интерес представляют выработки рабочих, обозначенных номерами: 5; 1; 4; 8; 7, поскольку их выработки отличаются наибольшими отклонениями. Тем самым выявляются передовые рабочие — номера: 1; 8; 7, обеспечивающие наибольшее повышение средней выработки (наибольшие положительные остатки) и отстающие, требующие особого внимания рабочие — номера: 5, 4 (наибольшие отрицательные остатки). В итоге положительные отклонения выработки большинства рабочих уравновешиваются отрицательными отклонениями небольшого числа рабочих, т. е. ∑ 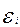 = 0.
= 0.
9.2.2.5. Многофакторный корреляционный и регрессионный анализ
Как известно, явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, т. е. эти явления многофакторны. Между факторами существуют сложные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний.
Многофакторный корреляционный и регрессионный анализ позволяет оценить меру влияния на исследуемый результативный
показатель каждого из включенных в модель (уравнение) факторов при фиксированном положении (на среднем уровне) остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя (важным условием является отсутствие между факторами функциональной связи).
Математически задача формулируется следующим образом. Требуется найти аналитическое выражение, наилучшим образом отражающее установленную теоретическим анализом связь независимых признаков с результативным, т. е. функцию
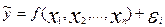
В условиях использования ЭВМ выбор аппроксимирующей математической функции осуществляется перебором решений, наиболее часто применяемых в анализе корреляции уравнений регрессии.
После выбора типа аппроксимирующей функции приступают
к многофакторному корреляционному и регрессионному анализу,
задачей которого является построение уравнения множественной
регрессии и нахождение его неизвестных параметров a0, a1,...,an.
Параметры уравнения множественной регрессии, как и в случае I парной регрессии, находят по способу наименьших квадратов. Затем с помощью корреляционного анализа осуществляют проверку адекватности полученной модели. Адекватную модель экономически интерпретируют.
9.2.2.6. Построение и статистический анализ
двухфакторной линейной модели
(трехмерной регрессии)
Для расчета параметров простейшего уравнения множественной линейной двухфакторной регрессии
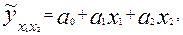
где 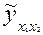 — расчетные значения зависимой переменной (результативного признака);
— расчетные значения зависимой переменной (результативного признака);
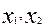 — независимые переменные (факторные признаки);
— независимые переменные (факторные признаки);
a0, a1, a2— параметры уравнения.
Построим следующую систему нормальных уравнений:


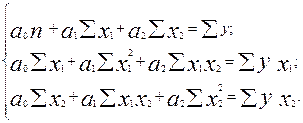 (9.13)
(9.13)
Параметры этой системы могут быть найдены, например, методом К. Гаусса.
9.2.2.7. Трехфакторные линейные регрессионные модели
В случае линейнойтрехфакторной связи уравнение регрессии имеет вид
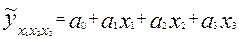
Для расчета параметров по способу наименьших квадратов используют следующую систему нормальных уравнений:
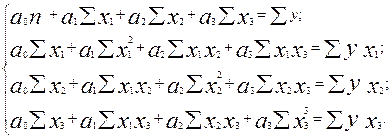 (9.14)
(9.14)
Чтобы получить эту систему, необходимо иметь таблицу значений следующих показателей:
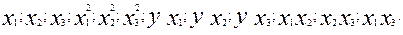
Для решения множественной регрессии с n-факторами
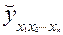 = a0+ a1x1+ a2 x2+... + an xn, система нормальных уравнений такова:
= a0+ a1x1+ a2 x2+... + an xn, система нормальных уравнений такова:
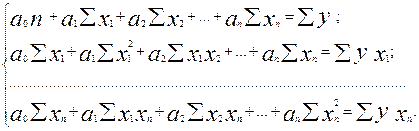 (9.15)
(9.15)
Вручную целесообразно выполнять построение и анализ только двух-, максимум трехфакторных моделей. Для n >3 все расчеты рекомендуется осуществлять на компьютерах по специальным программам, предусматривающим исчисление параметров уравнения и показателей, используемых для проверки его адекватности.
Многофакторный корреляционный и регрессионный анализ может быть использован в экономико-статистических исследованиях:
● для приближенной оценки фактического и заданного уровней;
● в качестве укрупненного норматива (для этого достаточно в уравнение регрессии подставить вместо фактических значений факторов их средние значения);
● для выявления резервов производства;
● для проведения межзаводского сравнительного анализа и выявления на его основе скрытых возможностей предприятий;
● для краткосрочного прогнозирования развития производства и др.
Построение и анализ трехмерной регрессионной модели рассмотрим на конкретном примере.
Пример 2. По выборочным данным, представленным в табл.9.3, о выработке деталей за смену 20 рабочими цеха требуется выявить зависимость производительности труда у от двух факторов: внутрисменных простоев x1 и квалификации рабочих x2.
Таблица 9.3
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1321; Нарушение авторских прав?; Мы поможем в написании вашей работы!