К расчету параметров и оценке линейной двухфакторной регрессионной модели

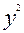
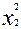
			yx1	yx2	x1x2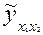
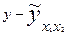
7396 7744 8836 ...	... 400 196	...	... 1540 1288	... 154 368	32 45 ... 40 56	89,0 91,2 91,7 ... 79,6 88,7	-3,0 -3,2 2,3 ... -2,6 3,3	9,0 10,24 5,29 ... 6,76 10,89
162 640			19 436				-	177,2

=8132; 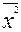= 141,5; 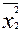= 17,1; = 971,8; = 364,9; = 41,1;

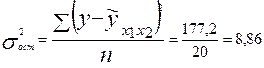
Составим систему нормальных уравнений:

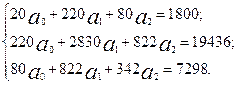
Решая данную систему методом К. Гаусса, получаем

a₀ =81,03; a₁ =-0,41; a₂ =3,37.

Уравнение множественной регрессии, выражающее зависимость производительности труда у от внутренних простоев x₁и квали­фикации рабочих x₂, примет вид:

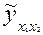= 81,03 - 0,41 x₁ + 3,37 x₂.

Вычислим по нему 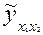и занесем полученные значения в табл.9.4.

После построения регрессионной модели необходимо исчис­лить различного рода характеристики тесноты связи между зависимой и независимой переменными: парные, частные и множест­венные коэффициенты корреляции, множественный коэффициент детерминации, а затем проверить адекватность данной модели.

9.2.2.8. Парные коэффициенты корреляции

Для измерения тесноты связи между двумя из рассматривае­мых переменных (без учета их взаимодействия с другими пере­менными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретация аналогичны методике расчета линейного коэффициента корре­ляции в случае однофакторной связи. Если известны средние квадратические отклонения анализируемых величин, то парные коэффициенты корреляции можно рассчитать проще по следующим формулам:

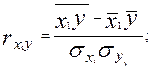(9.16)

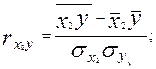(9.17)

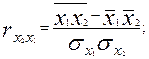(9.18)

Предварительно исчислим средние квадратические отклонения:

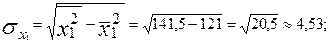
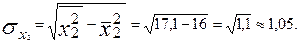
Тогда парные коэффициенты корреляции будут равны:

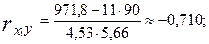
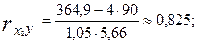
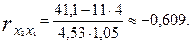
9.2.2.9. Частные коэффициенты корреляции

Однако в реальных условиях все переменные, как прави­ло, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при ус­ловии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества пере­менных, влияние которых исключается, частные коэффици­енты корреляции могут быть различного порядка: при исклю­чении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влия­ния двух переменных — второго порядка и т.д. Парный коэф­фициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.

Частный коэффициент корреляции первого порядка между при­знаками x₁и у при исключении влияния признака x₂ вычисляют по формуле:

(9.19)

то же – зависимость y от x₂ при исключении влияния x_1:

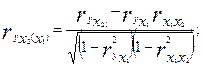(9.20)

Можно рассчитать взаимосвязь факторных признаков при устранении влияния результативного признака:

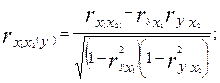(9.21)

где r - парные коэффициенты корреляции между соответствую­щими признаками.

Выполним расчет частных коэффициентов корреляции для нашего примера:

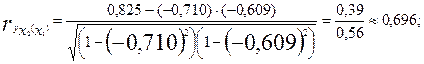
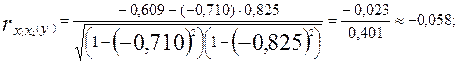
Итак, связь каждого фактора с изучаемым показателем при условии комплексного воздействия факторов слабее. Практически отсутствует связь между факторными признаками при элиминировании результативного показателя 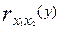=-0,058. Это вполне понятно — внутрисменные простои и квалификация рабочих никак не связаны между собой (если не прини­мать во внимание необходимость выполнения задания). Другое дело, если вопрос о выполнении задания: более квалифицированный рабочий допустит меньше внутрисменных простоев. Значение парного коэффици­ента корреляции, в этом случае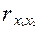= -0,609, подтверждает наличие довольно заметной обратной связи между этими факторами.

Изучение парных и частных коэффициентов корреляции по­зволяет отобрать наиболее существенные, значимые факторы.

На основе парных коэффициентов корреляции и средних квадратических отклонений можно легко рассчитать параметры уравнения линейной двухфакторной связи 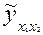= a₀+ a₁x₁+ a₂ x₂ по следующим формулам:

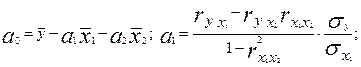
9.2.2.10.Совокупный коэффициент множественной

корреляции

Показателем тесноты связи, устанавливаемой между результа­тивными и двумя или более факторными признаками, является со­вокупный коэффициент множественной корреляции 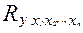. В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле:

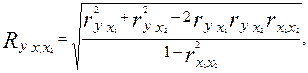(9.22)

где r — линейные коэффициенты корреляции (парные); подстроч­ные индексы показывают, между какими признаками они исчисляются.

Совокупный коэффициент множественной корреляции из­меряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах -1 до +1. Чем меньше наблюдаемые значения изучаемого показателя отклоня­ются от линии множественной регрессии, тем корреляционная связь является более интенсивной, а следовательно, значение R ближе к единице.

9.2.2.11. Совокупный коэффициент множественной детерминации

Совокупным коэффициентом множественной детерминации называется величина R², которая показывает, какая доля вариа­ции изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Значение совокупного коэффициента множественной детерминации на­ходится в пределах от 0 до 1. Поэтому, чем ближе R² к единице, тем вариация изучаемого показателя в большей мере характери­зуется влиянием отобранных факторов.

Для выявления, в нашем примере, тесноты связи производительно­сти труда с обоими факторами одновременно исчисляем совокупный ко­эффициент множественной корреляции:

Совокупный коэффициент множественной детерминации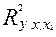 ⁼ 0,749 показывает, что вариация производительности труда на 74,9 % обусловливается двумя анализируемыми фактора­ми. Значит, выбранные факторы существенно влияют на пока­затель производительности труда. Таким образом, изучаемая с помощью многофакторного корреляционного и регрессионного анализа стохастическая связь между исследуемыми показателя­ми свидетельствует о целесообразности построения двухфакторной регрессионной модели производительности труда в виде линейного уравнения регрессии:

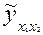=81,03-0,41 x₁+3,37х₂.

9.2.2.12. Многошаговый регрессионный анализ

Однако показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов. Поэтому только после проверки адекватности уравнения оно может быть пригодно, например, для выявления резервов по­вышения производительности труда.

Общая оценка адекватности уравнения может быть получе­на с помощью дисперсионного F-критерия Фишера. Примене­ние же в этих целях множественного коэффициента корреля­ции недопустимо ввиду того, что многофакторный регрессион­ный анализ оперирует случайными наблюдениями, но не обя­зательно распределенными по многомерному нормальному за­кону (этому закону должны подчиняться отклонения фактиче­ских значений функции от расчетных). Совокупный коэффи­циент множественной детерминации определяет только качест­во выравнивания по уравнению регрессии.

Проверку значимости уравнения регрессии производят на ос­нове вычисления F- критерия Фишера:

(9.23)

где m- число параметров в уравнении регрессии.

Полученное значение — критерия Fpacч сравнивают с критиче­ским (табличным) для принятого уровня значимости 0,05 или 0,01 и чисел степеней свободы ν₁ = m — 1 и ν₂ = n- m. Если оно окажется больше соответствующего табличного значения, то дан­ное уравнение регрессии статистически значимо, т. е. доля ва­риации, обусловленная регрессией, намного превышает случай­ную ошибку.

Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если Fpacч > Fтабл не менее чем в 4 раза.

Для оценки значимости коэффициентов регрессии при линей­ной зависимости у от x₁ и x₂ - (двух факторов) используют t-критерий Стьюдента при n-m-1 степенях свободы:

(9.24, a)

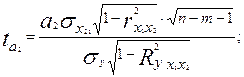(9.24, б)

Существенность совокупного коэффициента корреляции опре­деляют по формуле:

(9.25)

Значения оцениваемых a_1, a₂, 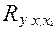берутся по модулю.

Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в каче­стве модели изучаемого показателя для последующего анализа.

Оценку значимости коэффициентов регрессии с помощью t- критерия используют для завершения отбора существенных факторов в процессе многошагового регрессионного анализа. Он заключается в том, что после оценки значимости всех коэф­фициентов регрессии из модели исключают тот фактор, коэф­фициент при котором незначим и имеет наименьшее значение критерия. Затем уравнение регрессии строится без исключен­ного фактора, и снова проводится оценка адекватности уравне­ния и значимости коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не ока­жутся значимыми, что свидетельствует о наличии в регрессион­ной модели только существенных факторов. В некоторых случа­ях расчетное значение t_расч находится вблизи t_табл, поэтому с точки зрения содержательности модели такой фактор можно ос­тавить для последующей проверки его значимости в сочетании с другим набором факторов.

Последовательный отсев несущественных факторов рас­смотренным выше приемом (или последовательным включе­нием новых факторов) составляет основу многошагового рег­рессионного анализа.

Проверим адекватность построенной двухфакторной модели про­изводительности труда по F-критерию Фишера:

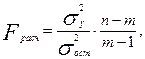
Табличное значение F-критерия при доверительной вероятности 0.95, т. е. (1-0,05) при н₁ = т - 1 = 2 - 1 = 1; н₂= n - т = 20 -2 = 18 со­ставляет 4,41.

Поскольку Fpacч > Fтабл уравнение регрессии 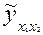= 81,03-0,41 x₁+3,37 x₂ следует признать адекватным.

Значимость a₁ , a₂ и 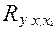оценим t-критерием Стьюдента:

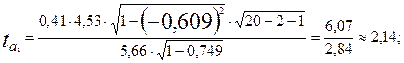
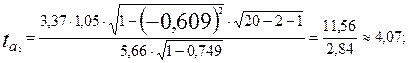
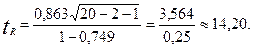
Табличное значение t-критерия при 5 %-ном уровне значимости и 17степенях свободы (n-m = 20—2—1 = 17) составляет 2,11. Так как со­ответствующие t_расч> t_табл, оба фактора a₁, a₂ и совокупный коэффици­ент корреляции 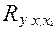следует признать значимыми (существенными).

Таким образом, построенная регрессионная модель производительно­сти труда 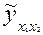= 81,03 -0,41 x₁+3,37 x₂ пригодна для практического

применения. Она может быть использована для выявления резервов повышения производительности труда.

9.2.2.13. Экономическая интерпретация многофакторной регрессионной модели

Анализ коэффициентов уравнения множественной регрес­сии: 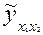=81,03 -0,41 x₁+3,37 x₂ позволяет сделать вывод о степени влияния каждого из двух факторов на показатель производительности труда. Так, параметр a₁ =-0,41 свидетель­ствует о том, что с увеличением продолжительности внутрисменных простоев на 1 мин следует ожидать снижения произ­водительности труда (дневной выработки деталей одним ра­бочим) на 0,41 шт. (обратная связь). Повышение же квали­фикации рабочего на 1 разряд может привести к увеличению выработки на 3,37 детали. Отсюда можно сделать соответст­вующие практические выводы и осуществить мероприятия, направленные на повышение производительности труда.

Однако на основе коэффициентов регрессии нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак, так как коэффициенты регрессии между собой не сопоставимы, поскольку они изме­рены разными единицами. На их основе нельзя также устано­вить, в развитии каких факторных признаков заложены наи­более крупные резервы изменения результативного показателя, потому что в коэффициентах регрессии не учтена вариа­ция факторных признаков.

Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эла­стичности Эi, а также бета-коэффициенты в_i и дельта коэффи­циенты Δ_i.

►Различия в единицах измерения факторов устраняют с помощью частных коэффициентов эластичности, которые рас­считывают по формуле:

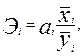(9.26)

где a_i — коэффициент регрессии при i-м факторе;

x_i — среднее значение i-го фактора;

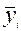— среднее значение изучаемого показателя.

Частные коэффициенты эластичности показывают, на сколь­ко процентов в среднем изменяется анализируемый показатель с изменением на 1% каждого фактора при фиксированном поло­жении других факторов.

►Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необ­ходимо учесть различия в степени варьирования вошедших в урав­нение факторов. Это можно сделать с помощью β-коэффициентов, которые вычисляют по формуле:

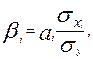(9.27)

где 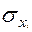— среднее квадратическое отклонение i-го фактора;

— среднее квадратическое отклонение показателя.

β -коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с

изменением соответствующего факторного признака на величину среднего квадратического отклонения..

►Исходя из соотношения и принимая во внимание, что коэффициент множественной детерминации 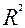есть доля изучаемых факторов в наличном приращении результативного показателя в анализируемой совокупности, можно сделать вывод, что произведение β_ir_i (1 ≤ i ≤ n) является показателем силы влияния соответствующего фактора на данный показатель.

Поделив произведение β_ir_i на коэффициент множест­венной детерминации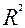, получим коэффициент, который показывает какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов. Обозначив этот коэффициент Δ_i получим

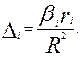(9.28)

Рассчитаем для нашего примера коэффициенты эластичности Эi, также коэффициенты β_i и Δ_i, дадим им экономическую интерпретацию:

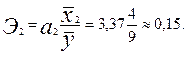
Анализ частных коэффициентов эластичности показывает, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор x₂ — повышение квалификации рабочих на 1% приводит к росту производительности труда на 0,15 %. Снижение же продолжительности внутрисменных простоев на 1% повышает про-изводительность труда только на 0,05%:

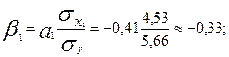
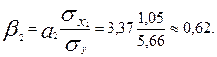
Анализ β_i -коэффициентов показывает, что на производительность труда наибольшее влияние из двух исследуемых факторов с учетом уровня их вариации способен оказать фактор x₂ — квалификация рабочих, так как ему соответствует наибольшее (по абсолютной величине) значение β –коэффициента:

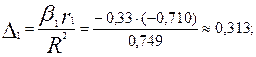
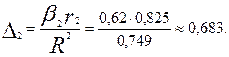
На основании анализа Δ_i - коэффициентов установлено, что наибольшая доля прироста производительности труда из двух анализируемых факторов может быть обеспечена развитием такого фактора, как повышение квалификации рабочих.

Таким образом, на основании частных коэффициентов эла­стичности Э_i, в_i - и Д_i -коэффициентов можно судить о резер­вах роста производительности труда, которые заложены в том или ином факторе.

Увеличение числа существенных факторов, включаемых в модель исследуемого показателя, позволяет выявить дополни­тельные резервы производства. Для этого могут быть использо­ваны трех-, четырех- (и т.д.), n-факторные регрессии.

9.3. Непараметрические методы

Применение корреляционного и регрессионного анализа тре­бует, чтобы все признаки были количественно измеренными. По­строение аналитических группировок предполагает, что количест­венным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных па­раметров распределения (средних величин и дисперсий).

Вместе с тем в статистике применяются также непарамет­рические методы, с помощью которых устанавливается связь между качественными (атрибутивными) признаками. Сфера их применения шире, чем параметрических, поскольку не требу­ется соблюдения условия нормальности распределения зависи­мой переменной, однако при этом снижается глубина исследо­вания связей. При изучении зависимости между качественны­ми признаками не ставится задача представления ее уравнени­ем. Здесь речь идет только об установлении наличия связи и измерении ее тесноты.

В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, пред­ставленными только группами с противоположными (взаимоис­ключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации.

Для расчета коэффициента ассоциации строится четырехклеточная корреляционная таблица, которая носит название табли­цы “четырех полей” и имеет следующий вид:

а	b	a+b
с	d	c+d
а+с	b+d	a+b+c+d

Применительно к таблице «четырех полей» с частотами a, b,c и d коэффициентассоциации выражается формулой:

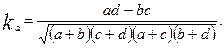(9.29)

Коэффициент ассоциации изменяется от —1 до +1; чем бли­же к +1 или — 1, тем сильнее связаны между собой изучаемые признаки.

Если k_a не менее 0,3, то это свидетельствует о наличии свя­зи между качественными признаками.

Пример 1. Имеющиеся данные о росте отцов и сыновей пред­ставлены в табл. 9.5.

Таблица 9.5

Дата добавления: 2014-01-06