Множественная (многофакторная) регрессия

Изучение связи между тремя и более связанными между собой признаками носит название множественной регрессии. При исследовании зависимостей методами множественной регрессии задача формулируется так же, как и при использовании парной регрессии, т.е. требуется определить аналитическое выражение связи между результативным признаком (У) и факторными признаками (х_1, х₂, …, х_к), найти функцию

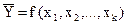
Построение моделей множественной регрессии включает 3 этапа:

· выбор формы связи (уравнения регрессии);

· отбор факторных признаков;

· обеспечение достаточного объема совокупности для получения оценок.

Практика построения многофакторных моделей показывает, что все реально существующие зависимости можно описать, используя 5 типов моделей:

1) линейная -

2) степенная -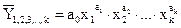

3) показательная -

4) параболическая -

5) гиперболическая -

где Y_1,2,3,…,k - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии;

х₁, х₂, …, х_к - факторные признаки;

а₀, а₁, …, а_к - параметры модели (коэффициенты регрессии)

Важным этапом построения является отбор и последующее включение факторных признаков. Сложность заключается в том, что все факторные признаки находятся в зависимости один от другого. Отбор признаков осуществляется при помощи двух методов: метода экспертных оценок и шаговой регрессии.

Метод экспертных оценок основан на расчете и анализе непараметрических показателей связи: ранговых коэффициентов корреляции Спирмена, Кендалла и конкордации.

Сущность метода шаговой регрессии заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициенты регрессии не изменяются (или меняются несущественно), то включение данного признака в уравнение регрессии необходимо. Если же при включении в модель факторного признака коэффициенты регрессии меняют величину, свой знак на противоположный, множественный коэффициент корреляции не возрастает, то данный факторный признак нецелесообразен.

Аналитическая форма выражения связи результативного признака и ряда факторных называется уравнением регрессии. Параметры уравнения могут быть найдены графически или аналогично парной корреляции - методом наименьших квадратов.

Для линейной зависимости уравнение для нахождения параметров имеет вид:

Для нахождения минимума функции продифференцируем выражение по каждому параметру и частные производные приравняем к нулю. Получаем систему уравнений:

Например, по параметру а₁ уравнение будет

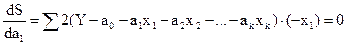
Делая соответствующие преобразования по всем значениям параметров а_i получаем

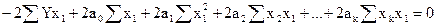
Отсюда имеем

В результате таких преобразований система нормальных уравнений с k неизвестными имеет вид:

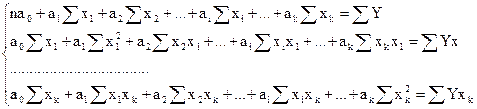
Оценка влияния каждого факторного признака на результативный может быть затруднена, если факторные признаки различны по своей сущности и имеют разные единицы измерения. В этих случаях все значения исследуемых признаков переводятся в стандарты по формуле:

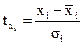
где х_i - значения признака в натуральном масштабе.

Уравнение множественной регрессии в стандартизованном масштабе следующее:

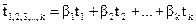(18)

Параметры многофакторной регрессии в стандартизованном масштабе определяются методом наименьших квадратов аналогично рассмотренному ранее.

Дата добавления: 2014-01-06