Формула Эйлера

Найдём число координат, определяющих положение абсолютно твёрдого тела.

Определить положение тела => определить координаты точки относительно некоторой системы отсчёта в момент времени.

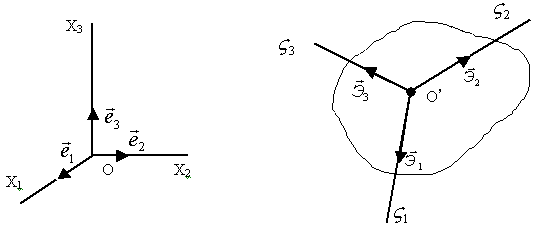
Рис.38.

Пусть Х₁ , Х₂, Х₃ – неподвижные оси (рис. 38); орты: 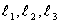[декартова система].

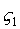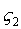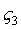, , - оси, жёстко связанные с телом; орты: 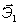, , 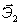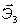- [декартова система].

Так как координаты точек относительно собственных осей 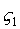,,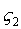 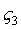не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х₁ , Х₂, Х₃.

Составим таблицу косинусов углов между осями Х и :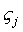

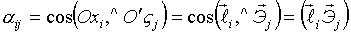
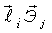- скалярное произведение.

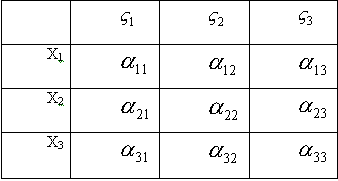
Так как системы координат ортогональны, то

скалярное произведени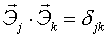е: , где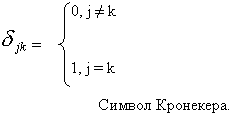

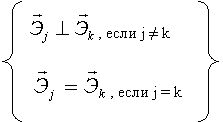
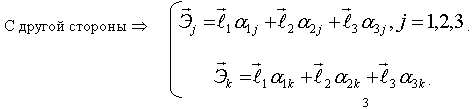
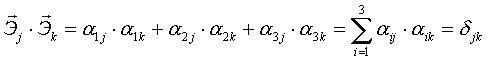
Итак: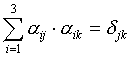

Число таких соотношений = 6 (Из 9 – ти в силу симметрии по jи k).

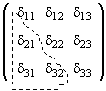Имеем 6 соотношений для 9 косинусов =>

3 косинуса , не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.

Кроме того => три координаты определяют положение точки О ’ – начало системы, , .

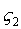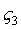Но 9 координат и 3 соотношение длин:

Это условия постоянства расстояний между точками в абсолютно твёрдом теле.

Выведем формулу Эйлера для распределения скоростей точек абсолютно твёрдого тела (рис. 39).

,

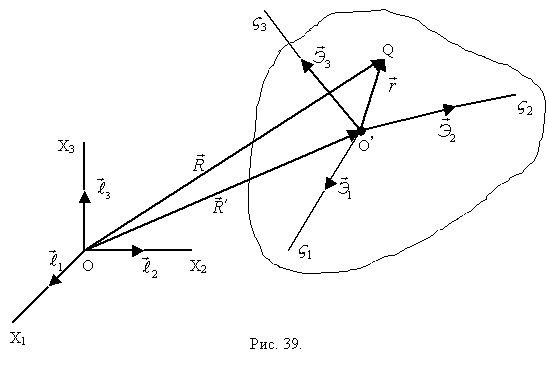
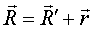1) ,

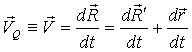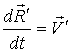- скорость точки О ^’,

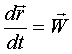- скорость точки Q во вращательном движении тела (так как длина 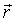постоянна).

Так как координаты 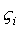точки Qпостоянны, то

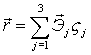
Тогда:

2) ,

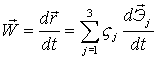где .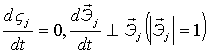

Скорость точки Q: .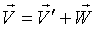

3) Выразим 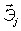и производные через направляющие косинусы :

.

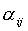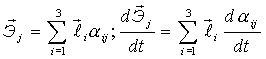Тогда: (в неподвижной системе).

4) Проекция 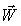на ось 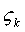(k= 1,2,3):

.

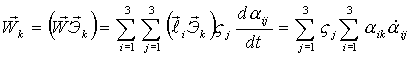Скорости точек во вращательном движении – линейные функции координат точек.

5) Получим более простую и наглядную форму закона распределения скоростей, используя свойства функции .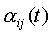

,

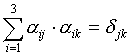Дифференцируем по t:

.

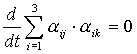По свойству производной от произведения:

при j= k => ,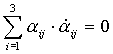

при j≠ k=> .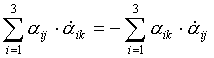

Свойства:

а) симметрия по kи j;

б) при j= k=>равенство «0»;

в) размерность t^-1, т. е. угловая скорость (угол в радианах), так как 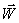- скорость.

г) различных только три =>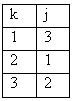

Покажем, что

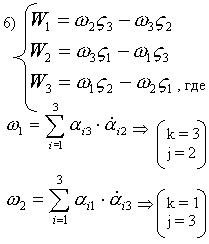
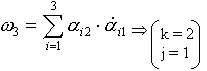
Действительно:

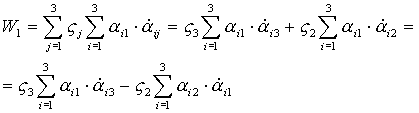
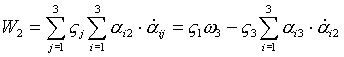
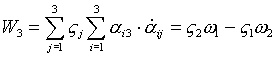- по аналогии.

Итак:

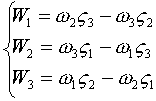
или:

7) 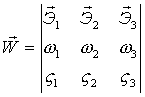, где 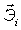- единичные вектора, жёстко связанные с телом.

Положим 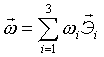- вектор, где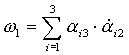

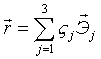
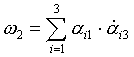
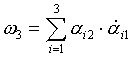
8) Тогда:

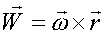
-Описывает распределение скоростей.

Назовём 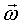вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О ^’ – осью мгновенного вращения, или мгновенной осью.

Таким образом, закон распределения скоростей точек абсолютно твёрдого тела в любом движении:

.

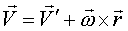Это формула Эйлера в векторной записи.

Контрольные вопросы:

1. Сколько координат определяют положение твёрдого тела в пространстве?

2. Что называется вектором мгновенной угловой скорости?

3. Напишите формулу Эйлера.

Дата добавления: 2014-01-06