Сложное движение точки

Для описания движения введём неподвижную и подвижную системы координат.

Рассмотрим движение точки М в подвижной системе отсчета , , 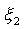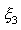(рис. 45). Для этого задают:

1) , где 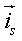- орты подвижной системы.

2) Движение системы относительно неподвижных осей.

Пусть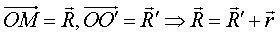

Найдем скорость точки М в неподвижной системе (дифференцированием):

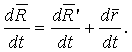
Очевидно:

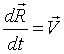- искомая скорость;

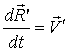- скорость начала подвижной системы.

Найдём с учётом ,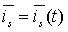

1)

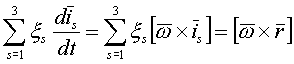
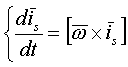, где 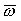- мгновенная угловая скорость вращения подвижной системы отсчета по формуле Эйлера

2) - назовем относительной производной

Итак:

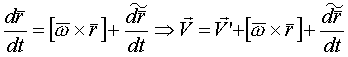
Если (т. е. нет относительного движения):

Поэтому:

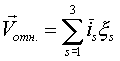- относительная скорость.

Переносная скорость (навязывается движением системы):

Это скорость того места, где в данный момент времени находится точка М.

Окончательно:

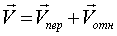
Найдем ускорение точки относительно неподвижной системы отсчета, если заданы относительные координаты и движение подвижной системы.

Дифференцируем:

:

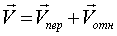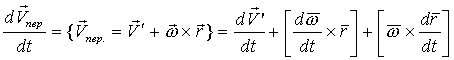
где 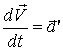- ускорение точки О’

здесь 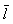- вектор от точки М к мгновенной оси под прямым углом (см. формулу Ривальса)

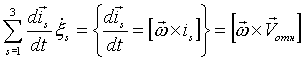
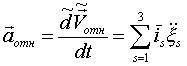- относительное ускорение (равно 0, если точка М движется в подвижной системе отсчета прямолинейно и равномерно).

Переносное ускорение – определяется как ускорение того места в подвижной системе отсчета, в которой точка М находится в рассматриваемый момент времени; вычисляется по формуле Ривальса:

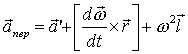
Ускорение Кориолиса:

Половина ускорения Кориолиса получена при дифференцировании по времени переносной скорости, а вторая половина – при дифференцировании относительной скорости.

- формула Кориолиса.

где ;

;

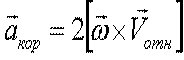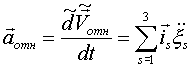
Формула Кориолиса позволяет вычислить абсолютное ускорение точки, если ее положение определяется координатами относительно подвижной системы отсчета.

Контрольные вопросы:

1. Что называется переносным и относительным движениями?

2. Напишите формулу скорости в сложном движении точки.

3. Из каких частей складывается ускорение Кориолиса?

Дата добавления: 2014-01-06