Дисперсия. На практике встречаются СВ, имеющие одинаковые математические ожидания, однако принимающие резко отличающиеся значения

На практике встречаются СВ, имеющие одинаковые математические ожидания, однако принимающие резко отличающиеся значения. У одних из этих СВ отклонения значений от математического ожидания небольшие, а у других, наоборот, значительны, т.е для одних рассеивание значений СВ вокруг математического ожидания мало, для других оно велико. Таким образом математическое ожидание характеризует поведение СВ далеко не полностью. Приведем следующий пример.

Пусть ДСВ Х и У заданы следующими рядами распределения

Х
Р	0.1	0.2	0.3	0.4

МХ = 2*0.1 + 3*0.2 + 4*0.3 + 5*0.4 = 4

У	-1
Р	0.2	0.5	0.2	0.1

МУ=(-1)*0.2+3*0.5+8*0.2+11*0.1=4

Отложим значения этих величин на числовых осях с одинаковым масштабом.

Приведенные рассуждения и пример свидетельствуют о целесообразности введения такой характеристики СВ, которая оценивала бы меру рассеивания значений СВ вокруг ее математического ожидания.

Х – МХ характеризует отклонение СВ от ее математического ожидания. Однако М(Х-МХ)=0, так как Х – МХ могут быть как положительные, так и отрицательные. Поэтому разумно ввести СВ (Х-МХ)² и рассмотреть ее математическое ожидание.

Опр. Математическое ожидание квадрата отклонения СВ Х от ее математического ожидания МХ называют дисперсией СВ Х и обозначают ДХ

ДХ = М(Х-МХ)².

Очевидно, что закон распределения СВ Х и (Х-МХ)² одинаковы.

Если Х - дискретная СВ, то математическое ожидание (Х-МХ)² равно

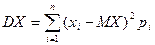
Если Х – непрерывная СВ, то

.

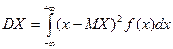Можно показать, что DX = M(X²)– M²(X).

Если СВ и ее математическое ожидание имеет одну и ту же размерность, то дисперсия имеет размерность квадрата СВ. Поэтому вводится среднее квадратичное отклонение 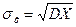- корень квадратный из дисперсии.

Задача. СВ задана следующим рядом распределения

Х
Р	0.1	0.2	0.4	0.2	0.1

Найти МХ и DX этой величины.

xi
pi	0.1	0.2	0.4	0.2	0.1
xipi	0.2	0.8	2.8	2.0	1.2	MX=7.0
xi-MX	-5	-3
(xi-MX)^2
(xi-MX)^2 pi	2.5	1.8		1.8	2.5	DX=8.6
xi^2
xi^2 pi	0.4	3.2	19.6	20.0	14.4	MX^2=57.6

MX = 7, DX =8.6

DX = MX² –(MX)² = 57.6 - 49 = 8.6.

Задача. СВ задана дифференциальной функцией распределения

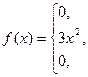
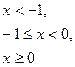Найти DX.

,

.

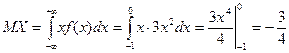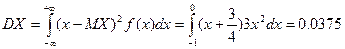Рассмотрим основные свойства дисперсии

1. Дисперсия алгебраической суммы двух независимых СВ Х и У равна сумме дисперсий этих величин, т.е. .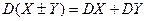

2. Дисперсия постоянной величины равна нулю DC = 0.

3. Постоянный множитель С СВ Х можно выносить за знак дисперсии, предварительно возведя его в квадрат .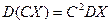

4. Дисперсия СВ Х равна разности между математическим ожиданием квадрата СВ и квадратом ее математического ожидания .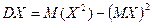

Следствие 1. Дисперсии СВ Х и центрированной СВ (Х – МХ) равны между собой

.

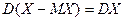Иногда бывает удобно использовать безразмерные центрированные СВ

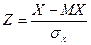- стандартная СВ.

Следствие 2. Математическое ожидание стандартной СВ (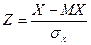)равно нулю, МZ=0

Следствие 3. Дисперсия стандартной СВ 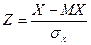равна 1,DZ = 1

Центрированная СВ геометрически означает перенос начала координат в точку с абсциссой, равной МХ.

Опр. Значение непрерывной СВ Х, при котором плотность распределения f(x) имеет наибольшее значение, называется модой М₀.

Модой дискретной СВ называется такое значение СВ, для которого вероятность максимальна: .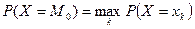

Опр. Число М_е,если оно удовлетворяет равенству

, будем называть медианой, т.е.

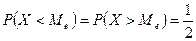- равновероятно, что СВ Х примет значение меньше М_е и больше М_е.

Дата добавления: 2014-01-06