Формула Бернулли. Тема 2. Повторные независимые испытания

Тема 2. Повторные независимые испытания

Сначала рассмотрим задачу – частный случай задач предыдущей темы. Наблюдение над решением позволит нам получить формулу, существенно упрощающую вычисления в аналогичных случаях.

Пример. Предполагается произвести 4 выстрела по мишени. Вероятность попадания при каждом выстреле считается известной и равной 0,7. Найти вероятность того, что

число попаданий в мишень будет:

а) равно 2;

б) не менее 2-х;

в) менее 4-х.

Решение. а) Принципиально эта задача не отличается от задачи о двух стрелках из § 1.6 (повторные испытания и здесь независимы) и может быть решена тем же способом. Введем обозначения, которые ниже будем использовать в подобных случаях. Число выстрелов по мишени обозначим через n (здесь 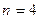), 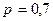– вероятность попадания в мишень при каждом выстреле, 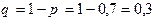– вероятность промаха при каждом выстреле, 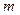– число попаданий. Требуется найти 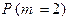, эту же вероятность обозначим через 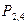. Перебирая все случаи, в которых число попаданий в мишень будет равно 2, получаем

.

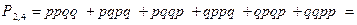
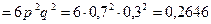В общем случае справедлива

Теорема. Пусть произведено n повторных независимых испытаний, в каждом из которых некоторое событие А наступает с вероятностью p. Тогда вероятность 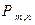того, что в этих n испытаниях событие А наступит 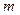раз, вычисляется по формуле

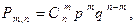
где 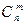– число сочетаний из n по , .

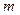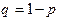Полученная формула носит название формулы Бернулли.

Завершим рассмотрение нашего примера.

б) Так как 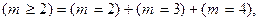то, применяя теорему сложения вероятностей для несовместных событий, получаем

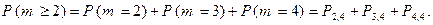
Первое слагаемое последней суммы найдено в п. а) данного примера. Аналогично для остальных:

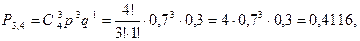
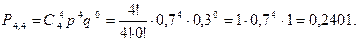
Окончательно имеем

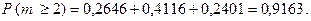
в) По аналогии с предыдущим пунктом задания,

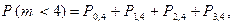
т.е. решение требует, вообще говоря, четырех применений формулы Бернулли. Однако возможно и более короткое решение. Действительно, события 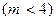и 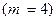– взаимно противоположны, следовательно

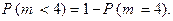
Вероятность 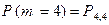найдена в п. б) примера. Таким образом, получаем

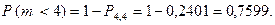
Домашнее задание:2.15, 2.16, 2.18.

Дата добавления: 2014-01-06