
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Следствия из интегральной теоремы Муавра-Лапласа
|
|
|
|
Свойства функции Лапласа
- Функция Лапласа нечетна:

- Функция Лапласа – монотонно возрастающая;
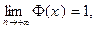
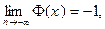 т.е. прямые
т.е. прямые 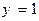 и
и 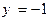
 являются горизонтальными асимптотами (правой и левой соответственно) графика
являются горизонтальными асимптотами (правой и левой соответственно) графика 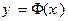 ; на практике полагаем
; на практике полагаем  при
при 
График функции Лапласа схематично изображен на рис. 2.

Пусть выполнены условия применимости интегральной теоремы Муавра-Лапласа.
Следствие 1. Вероятность того, что число 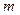 наступлений события А в n повторных независимых испытаниях будет отличаться от величины
наступлений события А в n повторных независимых испытаниях будет отличаться от величины 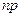 не более чем на
не более чем на 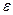 (по абсолютной величине), вычисляется по формуле
(по абсолютной величине), вычисляется по формуле
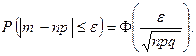
Следствие 2. Вероятность того, что доля 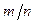 наступлений события А в n повторных независимых испытаниях будет отличаться от вероятности p наступления этого события в одном испытании не более чем на
наступлений события А в n повторных независимых испытаниях будет отличаться от вероятности p наступления этого события в одном испытании не более чем на  (по абсолютной величине), вычисляется по формуле
(по абсолютной величине), вычисляется по формуле

Пример. Подлежат исследованию 1000 проб руды. Вероятность промышленного содержания металла в каждой пробе равна 0,15. Найти границы, в которых с вероятностью 0,9973 будет заключено число проб руды с промышленным содержанием металла.
Решение. Искомые границы для числа 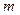 проб руды с промышленным содержанием металла (из данных 1000 проб) определяются величинами
проб руды с промышленным содержанием металла (из данных 1000 проб) определяются величинами  и
и  (см. интегральную теорему Муавра-Лапласа). Будем предполагать, что искомые границы симметричны относительно величины
(см. интегральную теорему Муавра-Лапласа). Будем предполагать, что искомые границы симметричны относительно величины 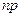 , где
, где 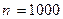 и
и  . Тогда
. Тогда 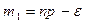 ,
, 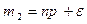 для некоторого
для некоторого  , и, тем самым, единственной определяющей неизвестной данной задачи становится величина
, и, тем самым, единственной определяющей неизвестной данной задачи становится величина 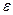 . Из следствия 1 и условия задачи следует, что
. Из следствия 1 и условия задачи следует, что
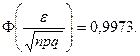
По таблице значений функции Лапласа найдем такое 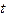 , что
, что 
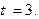
Тогда  и
и 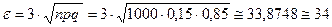 . Окончательно получаем искомые границы:
. Окончательно получаем искомые границы: 
 т.е. с вероятностью 0,9973 число проб руды с промышленным содержанием металла (из данных 1000 проб) попадет в интервал (116; 184).
т.е. с вероятностью 0,9973 число проб руды с промышленным содержанием металла (из данных 1000 проб) попадет в интервал (116; 184).
Пример. В лесхозе приживается в среднем 80% саженцев. Сколько саженцев надо посадить, чтобы с вероятностью 0,9981 можно было утверждать, что доля прижившихся саженцев будет находиться в границах от 0,75 до 0,85.
Решение. 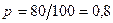 – вероятность прижиться для каждого из саженцев,
– вероятность прижиться для каждого из саженцев,  . Пусть
. Пусть 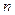 – необходимое число саженцев (искомая величина данной задачи) и
– необходимое число саженцев (искомая величина данной задачи) и 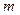 – число прижившихся из них, тогда
– число прижившихся из них, тогда 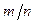 – доля прижившихся саженцев. По условию,
– доля прижившихся саженцев. По условию,

Данные границы для доли 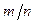 симметричны относительно величины
симметричны относительно величины 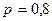 , поэтому неравенство
, поэтому неравенство 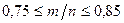 равносильно неравенству
равносильно неравенству 
Следовательно, вероятность 0,9981 – это та самая вероятность, которая вычисляется по следствию 2 из интегральной теоремы Муавра-Лапласа при 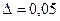 ,
, 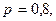
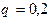 :
:

По таблице функции Лапласа найдем такое значение 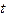 , что
, что  Это значение:
Это значение:  Тогда
Тогда

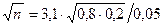 и
и
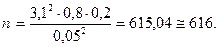
Заметим, что значение 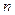 округлено до целых в большую сторону, чтобы обеспечить, как говорят, “запас по вероятности”. Кроме того, видно, что полученное значение
округлено до целых в большую сторону, чтобы обеспечить, как говорят, “запас по вероятности”. Кроме того, видно, что полученное значение 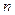 достаточно велико (более 100), поэтому применение интегральной теоремы Муавра-Лапласа для решения данной задачи было возможно.
достаточно велико (более 100), поэтому применение интегральной теоремы Муавра-Лапласа для решения данной задачи было возможно.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 8326; Нарушение авторских прав?; Мы поможем в написании вашей работы!