Закон распределения дискретной случайной величины

Тема 3. Дискретная случайная величина

Определение. Случайной величиной называется переменная, которая в результате испытания принимает то или иное числовое значение.

Пример. Число попаданий в мишень при 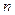выстрелах – случайная величина.

Пример. Рост наудачу взятого человека – случайная величина.

Определение. Случайная величина называется дискретной, если число ее возможных значений конечно или счетно.

(Напомним, что множество называется счетным, если его элементы можно перенумеровать натуральными числами.)

В этом смысле, число попаданий в мишень – пример дискретной случайной величины. Рост человека – непрерывная случайная величина (такие случайные величины будут рассмотрены ниже).

Для обозначения случайных величин будем использовать заглавные буквы латинского алфавита (возможно с индексами), например, и т.п.

Определение. Законом распределения дискретнойслучайной величины называется такая таблица, в которой перечислены все возможные значения этой случайной величины (без повторений) с соответствующими им вероятностями.

В общем виде закон распределения для случайной величины, например, :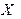

:				…
			…

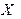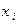
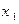
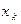
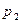
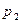
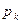
где

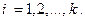
Из определения закона распределения следует, что события 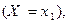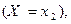…, 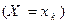образуют полную систему, поэтому (см. следствие из теоремы сложения вероятностей для несовместных событий в §1.6):

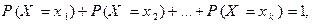
т.е.

Данное равенство называется основным свойством закона распределения.

Пример. Два стрелка одновременно выстреливают в мишень. Вероятность попадания для первого равна 0,6, для второго – 0,8. Составить закон распределения случайной величины – общего числа попаданий в мишень.

Решение. Возможные значения данной случайной величины: 0, 1, 2. Так же как в примере из §1.6, через и обозначим события, состоящие в попадании в мишень первого и второго стрелков (соответственно). Тогда аналогично упомянутому примеру получаем

Окончательно, закон распределения случайной величины имеет вид:

:
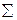
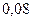
		0,44	0,48

Упражнение. В коробке 3 белых шара и 2 красных. Составить закон распределения случайной величины 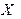– числа белых шаров среди 2-х извлеченных шаров.

Дата добавления: 2014-01-06