
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Арифметические операции над случайными величинами
|
|
|
|
Ответ.
Ответ.
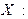
| 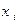
| 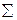
| |||

| 0,1 | 0,6 | 0,3 |
Пример. В коробке – 3 белых шара и 2 красных. Шары извлекаются последовательно до появления белого шара. Составить закон распределения случайной величины Х – числа извлеченных шаров.
Решение. Возможные значения данной случайной величины: 1, 2, 3. Событие 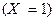 (из коробки будет извлечен один единственный шар) наступает тогда и только тогда, когда первый из шаров оказывается белым, т.к. появление именно белого шара является сигналом к прекращению последующих извлечений (см. условие). Поэтому
(из коробки будет извлечен один единственный шар) наступает тогда и только тогда, когда первый из шаров оказывается белым, т.к. появление именно белого шара является сигналом к прекращению последующих извлечений (см. условие). Поэтому
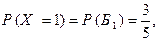
где событие 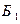 – первый из извлеченных шаров – белый. Событие
– первый из извлеченных шаров – белый. Событие 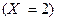 (из коробки будет извлечено ровно 2 шара) наступает тогда и только тогда, когда первый из извлеченных шаров оказывается красным, а второй – белым. Поэтому
(из коробки будет извлечено ровно 2 шара) наступает тогда и только тогда, когда первый из извлеченных шаров оказывается красным, а второй – белым. Поэтому
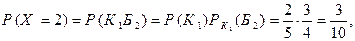
где событие 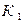 – первый из извлеченных шаров – красный,
– первый из извлеченных шаров – красный, 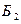 – второй шар – белый. Наконец событие
– второй шар – белый. Наконец событие 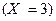 (из коробки будет извлечено 3 шара) наступает тогда и только тогда, когда первый шар – красный, второй – красный и третий – белый. Поэтому
(из коробки будет извлечено 3 шара) наступает тогда и только тогда, когда первый шар – красный, второй – красный и третий – белый. Поэтому
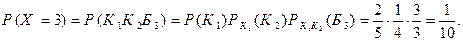
Окончательно искомый закон распределения имеет вид:
| Х: | 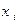
| 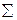
| |||

| 0,6 | 0,3 | 0,1 |
Упражнение. Имея 3 патрона, стрелок стреляет по мишени до первого попадания (или до израсходования патронов). Вероятность попадания при каждом выстреле равна 0,8. Составить закон распределения случайной величины Х – числа произведенных выстрелов.
| Х: | 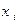
| 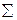
| |||

| 0,8 | 0,16 | 0,04 |
Пример. Стрелок стреляет в мишень 3 раза. Вероятность попадания при каждом выстреле равна 0,8. Составить закон распределения случайной величины Х – числа попаданий в мишень.
Решение. Возможные значения для числа попаданий: 0, 1, 2, 3. Вероятности того, что случайная величина Х примет эти значения вычисляются по формуле Бернулли при 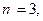
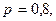
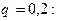
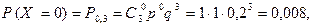
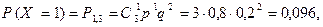
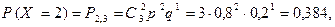
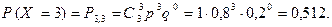
Окончательно искомый закон распределения имеет вид:
| Х: | 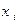
| 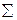
| ||||

| 0,008 | 0,096 | 0,384 | 0,512 |
Полученный закон распределения является частным случаем так называемого биномиального закона распределения (при 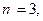
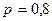 ).
).
Определение. Случайная величина Х имеет биномиальный закон распределения с параметрами 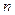 и
и 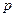 , если ее закон распределения имеет вид:
, если ее закон распределения имеет вид:
| Х: | 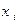
| … | 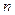
| , | |||

| 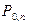
| 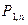
| 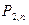
| … |  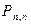
|
где вероятности 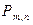 вычисляются по формуле Бернулли:
вычисляются по формуле Бернулли:
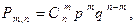
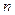 – положительное целое число,
– положительное целое число, 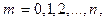
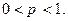
В пределе при 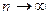 и
и 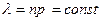 биномиальное распределение переходит в так называемое распределение Пуассона.
биномиальное распределение переходит в так называемое распределение Пуассона.
Определение. Говорят, что случайная величина Х имеет распределение Пуассона с параметром 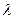 , если ее закон распределения имеет вид:
, если ее закон распределения имеет вид:
| Х: | 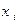
| … | , | |||

| 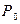
| 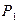
| 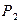
| … |
где
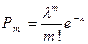 ,
,
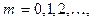
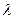 – положительное число.
– положительное число.
Убедимся в том, что для распределения Пуассона выполняется основное свойство закона распределения: 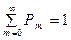 . Действительно, имеем
. Действительно, имеем

(см. курс математического анализа, разложение функции 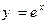 в ряд Маклорена).
в ряд Маклорена).
Домашнее задание. 3.25, 3.31, 3.36, 3.40, 3.45.
Определение. Случайные величины Х и Y называются равными, если их законы распределения точно совпадают, и для произвольного числа 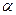 справедливо равенство:
справедливо равенство: 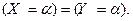
Пример. Пусть законы распределения случайных величин Х и Y имеют вид:
| Y: | 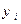
| . | ||

| 0,5 | 0,5 |
| X: | 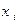
| ||

| 0,5 | 0,5 |
Эти случайные величины равны, если дополнительно справедливы равенства 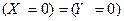 и
и 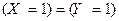 , т.е. случайная величина Х принимает значение 0
, т.е. случайная величина Х принимает значение 0
тогда и только тогда, когда случайная величина Y принимает значение 0, и аналогично со значением 1.
Произвольная случайная величина допускает умножение на число. Действительно, пусть закон распределения случайной величины Х имеет вид:
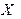 : :
| 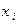
| 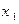
| 
| … | 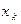
|

| 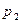
| 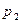
| … | 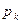
|
и 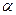 – некоторое число.
– некоторое число.
Определение. Случайной величиной 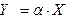 называется такая случайная величина, закон распределения которой имеет вид:
называется такая случайная величина, закон распределения которой имеет вид:
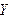 : :
| 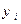
| 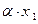
| 
| … | 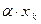
|

| 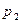
| 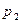
| … | 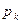
|
Пример. Пусть закон распределения случайной величины Х имеет вид:
| Х: | 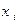
| |||
 
| 0,16 | 0,48 | 0,36 |
и 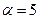 ,
, 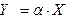 . Тогда закон распределения
. Тогда закон распределения 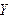 :
:
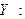
| 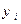
| |||
 
| 0,16 | 0,48 | 0,36 |
Можно придумать, например, следующую интерпретацию данному примеру. Заметим, что Х – биномиально распределена с параметрами 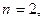
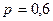 . Пусть Х – число попаданий в мишень при 2-х выстрелах, при каждом из которых попадание случается с вероятностью 0,6, и дополнительно известно, что за каждое попадание стрелку выплачивается вознаграждение в размере 5 ден. ед. Тогда Y – заработок стрелка.
. Пусть Х – число попаданий в мишень при 2-х выстрелах, при каждом из которых попадание случается с вероятностью 0,6, и дополнительно известно, что за каждое попадание стрелку выплачивается вознаграждение в размере 5 ден. ед. Тогда Y – заработок стрелка.
Определение. Случайные величины Х и Y называются независимыми, если для любых i и j события 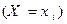 и
и 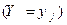 – независимы.
– независимы.
Пример. Пусть из коробки, в которой – 6 белых и 8 красных шаров, извлекается 1 шар. Рассмотрим случайные величины Х – число белых шаров, Y – число красных шаров из извлеченных. События, например, 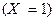 и
и 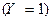 – несовместны, а поэтому – зависимы (см. § 1.6). Следовательно, и случайные величины Х и Y зависимы.
– несовместны, а поэтому – зависимы (см. § 1.6). Следовательно, и случайные величины Х и Y зависимы.
Определение. Суммой (разностью, произведением) случайных величин Х и Y называется такая случайная величина 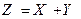 (
(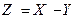 ,
, 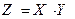 ), которая принимает значение
), которая принимает значение 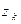 в некотором испытании, если значения
в некотором испытании, если значения 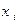 и
и 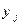 случайных величин Х и
случайных величин Х и 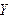 в этом испытании таковы, что
в этом испытании таковы, что 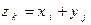 (
( ).
).
Пример. Пусть заданы законы распределения независимых случайных величин Х и Y:
| Х: | 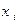
| Y: | 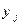
| ||||

| 0,4 | 0,6 | 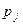
| 0,2 | 0,8 |
Составить закон распределения случайной величины 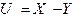 .
.
Решение. Удобно использовать вспомогательную таблицу вида:
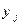 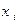
| ||
| –1 |
в каждой из центральных клеток которой записаны соответствующие произведения случайных величин X и Y. Такая таблица показывает, какие значения принимает случайная величина U и когда она принимает эти значения. Так 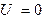 тогда и только тогда, когда
тогда и только тогда, когда 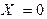 и
и 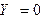 или
или 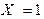 и
и 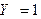 . Поэтому
. Поэтому
 .
.
Применяя теорему сложения вероятностей для несовместных событий, теорему умножения вероятностей – для независимых событий (по условию, случайные величины 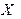 и
и 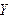 – независимы), получаем
– независимы), получаем
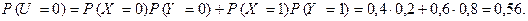
Для наступления каждого из двух оставшихся значений случайной величины U (-1 и 1) имеется по одной возможности. Например, 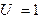 тогда и только тогда, когда
тогда и только тогда, когда 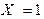 и
и 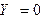 . Тогда получаем:
. Тогда получаем:
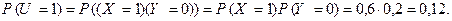
Аналогично,
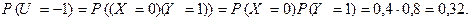
Окончательно, закон распределения случайной величины U имеет вид:
| U: | 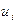
| –1 | ||
 
| 0,32 | 0,56 | 0,12 |
Упражнение. Составить законы распределения случайных величин 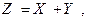
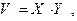

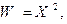
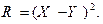
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1138; Нарушение авторских прав?; Мы поможем в написании вашей работы!