Параметры распределения дискретной случайной величины

Ответ.

Z:					V: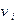
	0,08	0,44	0,48		0,52	0,48

W:		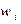		R: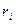
	0,4	0,6		0,56	0,44

Заметим, что закон распределения случайной величины Z фактически найден в примере § 3.1 о двух стрелках. Действительно, исходные независимые случайные величины X и Y данной задачи могут быть интерпретированы как числа попаданий в мишень первого и второго стрелка из § 3.1. Тогда 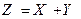– общее число попаданий, и закон распределения этой случайной величины и найден в упомянутом примере.

Пусть закон распределения дискретной случайной величины Х имеет вид

:				…
			…

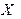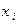
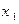
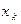
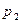
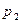
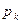
Определение. Математическим ожиданием дискретной случайной величины Х называется число М(Х), вычисляемое по формуле

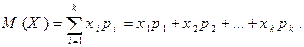
Математическое ожидание случайной величины есть число около которого группируются значения этой случайной величины.

Механическим аналогом математического ожидания дискретной случайной величины является центр масс (центр тяжести) системы точечных масс: если в точках числовой оси с абсциссами 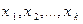расположены точечные массы , то абсцисса их центра масс находится точно по формуле для 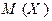, приведенной выше.

Пример. Пусть случайная величина Х биномиально распределена с параметрам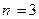и и 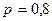(см. пример из § 3.1):

Х: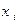
	0,008	0,096	0,384	0,512

Тогда

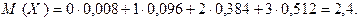
Дата добавления: 2014-01-06