Свойства характеристической функции

Имеется коалиционная игра Г=<I,{S_i}, 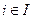, {H_i}>.

Опр. Вещественная функция v(k), определенная на семействе kI (всех подмножеств k из I), называется характеристической функцией.

Содержательно определенная характеристическая функция должна удовлетворять 3 свойствам:

1. Персональность

2. Супераддитивность

3. Дополнительность

Персональность: выигрыш участников коалиции определяется не только их числом, но и персональным составом коалиции. v()=0.

Супераддитивность: отражает заинтересованность двух групп, K и L, в коалиции: v(KL) v(K) + v(L)

Дополнительность: v(K) + v(I/K) = v(I), следовательно характеристическая функция показывает ресурс игры v(I) между коалицией К и лицами, не вошедшими в нее (I/K). А значит, если известны характеристические функции всех возможных коалиций, т.е. v(K) для 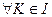, об игре известно все.

Надо так нормировать выигрыши всех игроков, чтобы v(I)=1. Тогда v(K)[0,1] .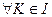

Игра, в которой v(K)[0,1] 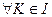, называется коалиционной игрой в 0,1-редуцированной форме.

ТЕОРЕМА. Всякая коалиционная игра Г приводится к единственной коалиционной игре в 0,1-редуцированной форме.

Рассмотрим некоторые свойства характеристической функции в 0,1-редуцированной коалиционной игре:

1. Всякая характеристическая функция является неотрицательной и неубывающей функцией.

2. Если K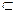L, то v(K) + v(L/K) 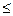v(L)

3. Всякая характеристическая функция в игре из n игроков, I={1,2,…,n}, описывается 2ⁿ-1 числом параметров, а при приведении игры в 0,1-редуцированную форму накладывается n+1 дополнительных связей, и, следовательно, получается (2ⁿ - n - 2) свободных параметров.

Рассмотрим, сколько будет свободных параметров в зависимости от числа игроков:

n=2 2²-2-2=0 v(1)=v(2)=0

v(1,2)=1

n=3 2³-3-2=3 v(1)=v(2)=v(3)=0

v(1,2)=c₃, v(1,3)=c₂, v(2,3)=c₁ 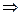3 параметра

v(1,2,3)=1

Пример. Рассмотренная ранее игра в 0,1-редуцированной форме (см. пример про продавца и покупателей):

v(Пр,П₁)=b-a || v()=v(П₁)=v(П₂)=v(П₁,П₂)=0

v(Пр,П₂)=c-a || v(Пр)=а-а=0

v(Пр,П₁)=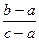

v(Пр,П₂)=1

v(Пр,П₁,П)=1

Если при анализе 0,1-редуцированной игры учитывать свойство дополнительности, то на наибольшее число параметров накладывается еще одно условие. Содержательно игру в 0,1-редуцированной форме можно определить, если число участников n3.

После определения выигрыша коалиции возникает задача дележа выигрыша между участниками коалиции. Задача определения справедливых дележей рассматривается в кооперативных играх.

Дата добавления: 2014-01-06