
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Допустимые стратегии в статистических играх
|
|
|
|
Допустим, что рассматривается смешанная стратегия:
P(x)= (a).
(a).
Возможно два случая:
Нельзя найти  ’(а) — другая стратегия, когда потери:
’(а) — другая стратегия, когда потери:
L(V,  ’)
’)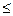 L(V,
L(V,  ), V
), V Z
Z
Если такая стратегия  ’(a) существует, то стратегия
’(a) существует, то стратегия  (а) недопустима.
(а) недопустима.
 (а) a
(а) a = x
= x
 (a
(a )
)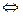 p(x
p(x )
)
Стратегия  (а) — допустимая, если нельзя найти другую стратегию
(а) — допустимая, если нельзя найти другую стратегию  ’(a): L(V,
’(a): L(V,  ’)
’)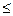 L(V,
L(V,  ) — условие допустимости стратегии
) — условие допустимости стратегии  (а).
(а).
Допустимая стратегия не обязательно является предпочтительной. Допустимую стратегию удобно рассматривать в рамках S-игры.
Если V=(V V
V ), то потери можно рассмотреть на плоскости.
), то потери можно рассмотреть на плоскости.
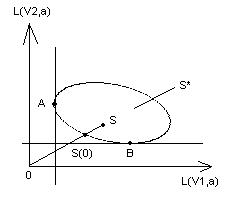
Множество значений этих потерь можно сопоставить с выпуклой линейной оболочкой S*.
Рассмотрим некоторую точку S S*, проведём отрезок из начальных координат в эту точку. Очевидно, что все точки, расположенные на этом луче и множество S* будут давать потери, меньшие, чем потери S. Наименьшие потери будут а точке S
S*, проведём отрезок из начальных координат в эту точку. Очевидно, что все точки, расположенные на этом луче и множество S* будут давать потери, меньшие, чем потери S. Наименьшие потери будут а точке S , которая является пересечением луча и нижней левой границы выпуклой оболочки.
, которая является пересечением луча и нижней левой границы выпуклой оболочки.
Допустимыми могут быть стратегии, принадлежащие участку линейной оболочки, который является дугой AB. Все стратегии, которые определяются точками линейного множества S*, не принадлежащие её левой нижней границе, можно исключить из рассмотрения. А точки, принадлежащие дуге АВ, в некотором смысле эквивалентны, т. к. при перемещении по этим точкам можно уменьшить потери в одном состоянии и увеличить в другом (сразу всё уменьшить невозможно).
Пример: «задача о технологической линии»
Нижняя левая граница состоит из точек C , C
, C и С
и С
WC +(1-W)C
+(1-W)C WC
WC +(1-W)C
+(1-W)C

Смешанная стратегия  (а) = (W, 1-W, 0),
(а) = (W, 1-W, 0),  (a) = (0, W, 1-W)
(a) = (0, W, 1-W)
Определим потери статистика для этих стратегий: L(V ,
,  ) = W*0 + 1*(1-W) = 1-W, L(V
) = W*0 + 1*(1-W) = 1-W, L(V ,
,  ) = 5*W + 3(1-W) = 3 + 2W
) = 5*W + 3(1-W) = 3 + 2W
L(V ,
,  ) = 1*W + 3(1-W) = 3 – 2W
) = 1*W + 3(1-W) = 3 – 2W
L(V ,
,  ) = 3W + 2(1-W) = 2+ W
) = 3W + 2(1-W) = 2+ W
Рассмотрим возможные пути выбора смешанных стратегий статистика.
1. Принцип минимакса (min max);
2. Байесовский принцип.
Принцип минимакса ориентирует статистика на выбор такой смешанной стратегии  (а), при которой его потери в наихудшем состоянии природы минимальны.
(а), при которой его потери в наихудшем состоянии природы минимальны.
Применим этот принцип для выбора W в задаче.
1 случай:
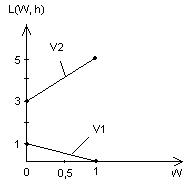
В наихудшем состоянии природы эти потери определяются прямой V : W = 0
: W = 0  *(0 1 0), потери равны 3.
*(0 1 0), потери равны 3.
2 случай:
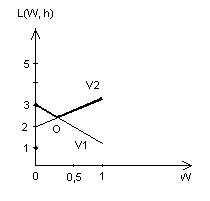 3 -2W = 2 + W
3 -2W = 2 + W
1 = 3W; W = 1/3
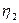 * (0 1/3 2/3); V = 7/3 (цена игры).
* (0 1/3 2/3); V = 7/3 (цена игры).
В наихудшем состоянии природы потери определяются верхней границей, минимум в точке О.
Иногда значение функции потерь удобно приводить к определённому нулевому уровню. Очевидно, для нахождения состояния природы L(V , a
, a )
)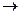
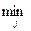 L(V
L(V , a
, a )
)
Этот минимум определяет минимальные затраты, которые может понести статистик при каждом состоянии природы.
L’(V,  ) = L(V,
) = L(V,  ) -
) - 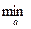 L(V, a)
L(V, a)
В предыдущей задаче о ПДК потери определялись бы следующим образом:
| V | a1 | a2 | a3 |
| V1 | 1-0=1 | 3-0=3 | |
| V2 | 5-2=3 | 3-2=1 | 2-2=0 |
Очевидно, что принцип минимакса можно применять и для дополнительных потерь.
Байесовский принцип направлен на принятие решения, исходя из априорных оценок вероятностей состояния природы.
q(V) 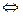
 (V)
(V)
Если q — априорная вероятность состояния природы, то можно говорить о потерях:
L( ,
,  ) =
) = 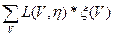
 Матрица потерь статистика в игре:
Матрица потерь статистика в игре:
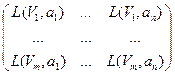 *
*  =
= 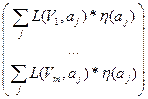
 (V
(V ), i =
), i = 
L( ,
,  ) =
) = 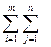 L(V
L(V , a
, a ) *
) *  (a
(a ) *
) *  (V
(V )
)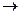 min
min
Наилучшей стратегией будет та, при которой байесовские потери L( ,
,  ) будут минимальными. Аналогично можно применить байесовский принцип при дополнительных потерях.
) будут минимальными. Аналогично можно применить байесовский принцип при дополнительных потерях.
Пример: (та же задача)
1 ситуация:
 (V
(V ) = 0,6. Найдём оптимальную байесовскую стратегию в этой задаче.
) = 0,6. Найдём оптимальную байесовскую стратегию в этой задаче.
 (V
(V ) = 0,4
) = 0,4
L( ) = (1-W)*0,6 + (3 + 2W)*0,4 = 1,8 + 0,2W
) = (1-W)*0,6 + (3 + 2W)*0,4 = 1,8 + 0,2W 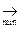 1,8 при W = 0.
1,8 при W = 0.
 (0, 1, 0) – нужно применять вторую технологию.
(0, 1, 0) – нужно применять вторую технологию.
2 ситуация:
L( ) = 0,6*(3-2W) + 0,4(2 + W) = 2,6 – 0,8W
) = 0,6*(3-2W) + 0,4(2 + W) = 2,6 – 0,8W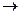 min W=1
min W=1
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 376; Нарушение авторских прав?; Мы поможем в написании вашей работы!