Байесовской стратегии

Геометрическая интерпретация выбора

Пусть имеется игра с двумя состояниями природы L(V, a) и L(V, a)

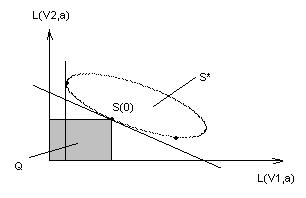
(a) — смешанная стратегия статистика.

Построим вспомогательное множество, состоящее из всех точек, лежащих левее и ниже S.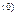

Считают, что множества S* и Q выпуклые и не пересекаются. Следовательно, можно провести прямую, разделяющую два этих множества. Эта прямая должна проходить через точку S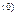. Эта прямая является опорной.

Эта прямая:

1. Вертикальная;

2. Горизонтальная;

3. Имеет отрицательный наклон

Уравнение y = -kx + c, k>0

ax + by = c’*k >0

a = k/(k+1); b = 1/(k+1); c’ = c/(k+1); a, b, c >0; a + b = 1

Величины a и b можно толковать как вероятности состояний природы

a = (V) = W; b = (V) = 1-W; (1-W)*y = c’.

Т. о. величина c’ определяет средние байесовские потери статистика L() при априорных вероятностях W и (1-W) состояний природы. Нетрудно убедиться в том, что эти значения c’ являются минимальными для всех значений L(), т. к. при c’’ > c’(справа от прямой) эта прямая не будет иметь общих точек с нижней левой границей и будет соответствовать недопустимым стратегиям статистика. Если c’’ < c’, то тоже не будет общих точек с S* (слева от прямой).

Т. о. можно утверждать, что каждая допустимая стратегия статистика является байесовской при некоторых вероятностях состояния природы.

Можно расмотреть обратную задачу: пусть известны W и (1-W) — вероятности состояния природы, Vи V. Требуется определить точку S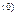S*, соответствующую этим значениям вероятности. Тогда априорные вероятности W и (1-W) определят некоторую прямую W*x + (1-W)*y = c/

x/(1-W) + y/W = c’

c’ = c/W(1-W), W(0,1)

Если менять C’, то прямая будет перемещаться параллельно самой себе.

Далее рассмотрим выпуклую линейную оболочку дискретного множества чистых стратегий статистика S*.

Нижняя левая граница определяется двумя линиями. Меняя C’ можно добиться того, чтобы эта прямая касалась множества S*.

S* — многоугольник с вершинами, соответствующими чистым стратегиям статистика. В этом случая прямая должна проходить хотя бы через одну из его вершин. Следовательно, для любых чисел W и (1-W), являющихся априорными вероятностями состояния природы, всегда существует хотя бы одна байесовская стратегия статистика, которая является чистой. Это обстоятельство при поиске байесовских решений позволяет ограничиться анализом допустимых чистых стратегий статистка, а не рассматривать бесконечное число его смешанных стратегий.

Дата добавления: 2014-01-06