Кривая нормального распределения и ее свойства

В результате многочисленных экспериментов было установлено, что при механической обработке деталей теоретическая частость для линейных размеров определяется следующим выражением

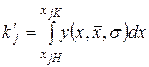. (13.13)

В нем

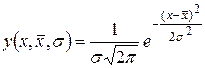(13.14)

называется плотностью распределения случайной величины. Функция, представленная этим выражением, называется законом нормального распределения. График этой функции приведен на рис.13.2 и называется кривой нормального распределения.

Из формулы (13.14) следует, что плотность распределения случайной величины для линейных размеров имеет размерность обратную длине, т.к. среднее квадратическое отклонение имеет данную размерность. В этой связи плотность распределения следует рассматривать, как величину, показывающую насколько велика вероятность появления случайной величины в окрестности некоторой точки на отрезке единичной длины. В окрестностях 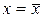плотность распределения максимальная, т.е. вероятность появления случайной величины в окрестностях этой точки максимальная. С увеличением разности 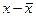плотность распределения уменьшается.

Чтобы лучше усвоить понятие плотности распределения, можно провести аналогию с плотностью вещества, которая определяется как масса, содержащаяся в единице объема. Представим себе стержень, плотность вещества которого меняется по длине согласно некоторому закону. Тогда, чтобы определить массу участка стержня, необходимо вычислить определенный интеграл от плотности его материала в пределах этого участка. Следуя этой аналогии, чтобы определить вероятность появления случайной величины 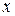в некотором интервале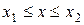, плотность распределения которой подчиняется нормальному закону, необходимо вычислить интеграл

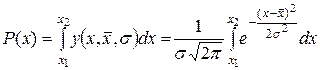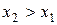, . (13.15)

Геометрически 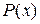представляет собой площадь фигуры на отрезке 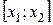под кривой нормального распределения.

Для достаточно узкого интервала согласно теореме о среднем

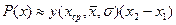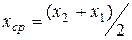; . (13.16)

Кривая нормального распределения имеет следующие свойства:

1. Ось 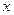является асимптотой для ее ветвей.

2. При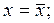

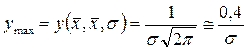. (13.17)

3. Кривая имеет две точки перегиба 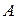и 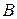, которые находятся на расстоянии 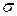от оси симметрии (рис.13.2). Ординаты их равны

. (13.18)

4. Если случайная величина подчиняется нормальному закону распределения и может принимать любые численные значения в интервале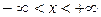, то

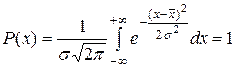. (13.19)

Это свойство вытекает из положения, что вероятность появления случайной величины в интервале 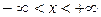равна единице.

Положение кривой относительно начала координат, и ее форма определяются двумя параметрам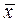и и 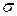. С изменением 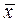форма кривой остается прежней. Изменяется ее положение относительно начала координат (рис. 13.3). С изменением 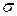центр кривой остается на прежнем месте. Изменяется ее форма (рис.13.4). С увеличением 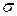кривая растягивается и уменьшается по высоте. Таким образом 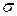определяет степень рассеяния случайной величины.

Дата добавления: 2014-01-06