
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методика построения эмпирической кривой распределения
|
|
|
|
Анализ точности методом кривых распределения
Основой метода является построение кривых распределения случайных значений геометрических размеров.
Пусть имеется партия из 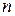 деталей, которую будем называть объемом выборки. Допустим размеры деталей в этой партии являются случайными величинами. Эмпирическая кривая распределения отражает закон распределения размеров деталей в пределах поля их рассеяния. Эта кривая строится в следующей последовательности:
деталей, которую будем называть объемом выборки. Допустим размеры деталей в этой партии являются случайными величинами. Эмпирическая кривая распределения отражает закон распределения размеров деталей в пределах поля их рассеяния. Эта кривая строится в следующей последовательности:
1. Производится измерение деталей. Для этого используется прибор с ценой деления шкалы  .
.
Ценой деления называется разность значений измеряемой величины между двумя соседними отметками шкалы. Рекомендуется выбирать цену деления, а следовательно, и прибор для измерения, в зависимости от объема выборки по следующему правилу


 (13.1)
(13.1)
где 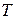 – допуск на размер.
– допуск на размер.
2. Из совокупности 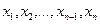 размеров определяются наибольший
размеров определяются наибольший  и наименьший
и наименьший  размеры, а также их разность, которая называется размахом выборки
размеры, а также их разность, которая называется размахом выборки
 . (13.2)
. (13.2)
3. Размах выборки разбивают на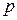 равных интервала. Величину интервала определяют по формуле
равных интервала. Величину интервала определяют по формуле
 . (13.3)
. (13.3)
Полученное значение округляют до величины кратной  по правилу
по правилу
 g = 1,2,3,…. (13.4)
g = 1,2,3,…. (13.4)
Таким образом,  должен превышать цену деления, по крайней мере, в два раза.
должен превышать цену деления, по крайней мере, в два раза.
4. За начало первого интервала принимают величину
 (13.5)
(13.5)
Для каждого последующего под номером 
 (13.6)
(13.6)
Конец первого интервала определяется значением
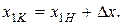 (13.7)
(13.7)
Для каждого последующего
 (13.8)
(13.8)
Очевидно, что

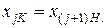 (13.9)
(13.9)
Для последнего интервала имеем  , где
, где 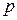 - номер последнего интервала.
- номер последнего интервала.
Таким образом, первый интервал содержит  Последний –
Последний –  .
.
5. Определяют количество деталей, размеры которых попадают в тот или иной интервал  . Это количество обозначают
. Это количество обозначают 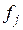 и называют частотою. Отношение
и называют частотою. Отношение  называется частостью.
называется частостью.
6. Полученные результаты оформляют в виде таблицы 8.1 распределения размеров. В качестве примера заполнения таблицы примем: количество деталей в партии 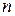 = 120, количество интервалов
= 120, количество интервалов 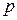 =10, количество частот по интервалам:
=10, количество частот по интервалам:
Таблица 8.1
Распределение размеров
| № интервала | Границы интервала, мм | Регистрация частот |
Частота,

|
Частость,
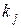
| |

| 
| ||||

| 
| ХХ | 0,0166 | ||

| 
| Х | 0,0083 | ||
| 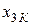
| ХХХХХ | 0,0416 | ||

| 
| ХХХХХХХХХХХХХХХХХХХХ | 0,1666 | ||

| 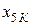
| ХХХХХХХХХХХХХХХХХХ | 0,1500 | ||

| 
| ХХХХХХХХХХХХХХХХХХХХХХХХХХХХ | 0,2333 | ||

| 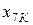
| ХХХХХХХХХХХХХХХХХХХХХХХХХХХ | 0,2250 | ||

| 
| ХХХХХХХХХХХХХ | 0,1083 | ||

| 
| ХХХХ | 0,0333 | ||
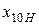
| 
| ХХ | 0,0166 | ||
| Итого: | 0,9996 |
 =2;
=2;  =1;
=1;  =5;
=5; 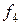 =20;
=20;  =18;
=18; 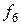 =28;
=28;  =27;
=27;  =13;
=13;  =4;
=4;  =2.
=2.
Из таблицы следует, что
 ;
; 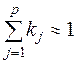 . (13.10)
. (13.10)
Очевидно, что 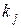 можно рассматривать как величину, близкую к вероятности попадания размера детали из партии в тот или иной интервал.
можно рассматривать как величину, близкую к вероятности попадания размера детали из партии в тот или иной интервал.
6. По данным таблицы 8.1 строят ступенчатый график, состоящий из прямоугольников шириною  , высотою
, высотою  или
или 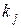 . Этот график называется гистограммой распределения. Если соединить середину верхней стороны каждого прямоугольника отрезками прямых, то получим ломаную линию, которая называется эмпирической кривой распределения или полигоном (рис.8.1).
. Этот график называется гистограммой распределения. Если соединить середину верхней стороны каждого прямоугольника отрезками прямых, то получим ломаную линию, которая называется эмпирической кривой распределения или полигоном (рис.8.1).

Графическая интерпретация полученных результатов позволяет сделать вывод, что размеры деталей группируются около некоторой центральной величины (центра группирования), причем, чем больше отличие между этой величиной и фактическим размером, тем меньше частота регистрации этого размера. Эта центральная величина называется средним арифметическим значением случайных величин и определяется по следующей формуле
 ;
;  (13.11)
(13.11)
Очевидно, что  - значение случайной величины в середине
- значение случайной величины в середине  - го интервала.
- го интервала.
Другой характеристикой кривой распределения случайных величин, является среднее квадратическое отклонение случайных величин от среднего арифметического значения, которое определяется по формуле
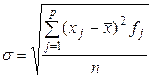 . (13.12)
. (13.12)
Если постепенно увеличивать размер партии, то ломаная линия будет приближаться к холмообразной кривой, аналогичной той, которая представлена на рис.8.1.2. и рис.8.1.7.

Тогда частота  и частность
и частность 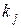 на каждом интервале будут стремиться к некоторым значениям
на каждом интервале будут стремиться к некоторым значениям  и
и  на данном интервале, которые в дальнейшем будем называть теоретической частотой и теоретической частостью.
на данном интервале, которые в дальнейшем будем называть теоретической частотой и теоретической частостью.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 2459; Нарушение авторских прав?; Мы поможем в написании вашей работы!