Вынужденные колебания. Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо компенсировать потери энергии при помощи какого-либо периодически

Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо компенсировать потери энергии при помощи какого-либо периодически действующего фактора, изменяющегося по гармоническому закону 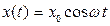. При механических колебаниях таким фактором является вынуждающая сила .

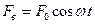Дифференциальное уравнение вынужденных колебаний системы имеет вид:

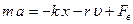или 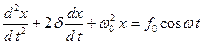, (1.8.20)

где 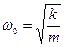– циклическая частота свободных незатухающих колебаний;

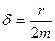– коэффициент затухания; .

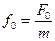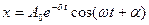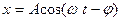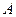Это линейное неоднородное дифференциальное уравнение. Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Можно показать, что частное решение имеет вид , где и 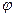задаются формулам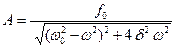и

и 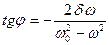. (1.8.21)

Амплитуда 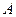вынужденных колебаний максимальна при частоте 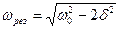, которая

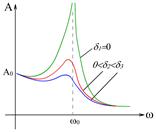Рис.5.7

называется резонансной частотой 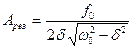. Если 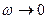, то все кривые приходят к одному и тому же, отличному от нуля, предельному значению , называемому статическим отклонением. Если 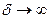, то все кривые асимптотически стремятся к нулю. Если 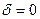, т. е. затухания колебаний нет, то 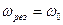, и амплитуда при этом становится бесконечно большой. Поскольку в реальных системах 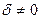, амплитуда достигает своего максимального значения и остается конечной. Приведенная на рис. 5.7 совокупность кривых называется резонансными кривыми.

Лекция 3.

IX. Волны.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). Механическими (упругими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Дата добавления: 2014-01-06