Закон полного тока

Циркуляцией вектора 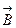, по заданному замкнутому контуру называется интеграл

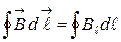, (4.6.1)

где 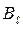= Вcosa - составляющая вектора 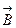в направлении касательной к контуру, 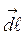- вектор элементарной длины контура (в направлении обхода контура), a - угол между векторам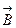и и 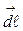.Наиболее просто вычислить этот интеграл для магнитного поля, прямого проводника с током. Пусть прямой проводник перпендикулярен плоскости чертежа, ток направлен к нам (рис.20.14). Замкнутый контур представим в виде окружности радиуса r.

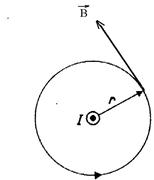Рис.20.14

Вектор 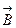в каждой точке этого контура одинаков по модулю и направлен по касательной к окружности (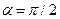). Циркуляция вектора 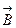равна:

. (4.6.2)

Если контур тока не охватывает, то циркуляция вектора 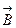равна нулю. Можно показать, что формула (4.6.2) справедлива и для тока, текущего по проводнику произвольной формы. Сформулируем закон полного тока для магнитного поля в вакууме: циркуляция вектора 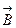по произвольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватываемых этим контуром.

(4.6.3)

где n – общее число проводников с током, охватываемых контуром произвольной формы. Если ток охватывает контур несколько раз, то он должен учитываться столько же раз. Необходимо соблюдать правило знаков: положительным считается ток, направление которого связано с направлением обхода контура известным правилом правого винт

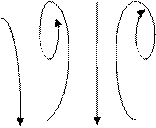I₁ I₂ I₃ I₄

Рис.20.15

На рис (20.15) изображен контур, охватывающий несколько токов. Направление обхода - против часовой стрелки. Алгебраическая сумма токов:

.

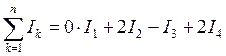Дата добавления: 2014-01-06