Принцип относительности

Рассмотрим две инерциальные системы отсчета: неподвижную 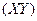и подвижную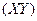,которые движутся со скоростью .

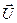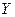
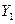
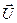
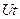
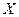
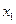
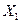
Тогда координаты одной и той же точки будут связаны соотношением:

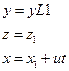- преобразования Галилея.

При выводе этих формул, мы учитываем, что в классическом приближении, время в обеих системах отсчета одинаково.

Тогда:

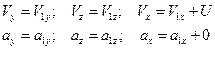
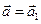
Уравнение движения в системе 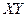имеет вид: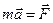

Уравнение движения в системе 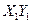имеет вид:

В классическом приближении, предполагалось, что масса точки и силы не зависят от выбора системы отсчета (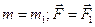), так как из преобразований Галилея следует: 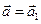, то получаем уравнение движения в системе 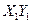совпадает с уравнением движения точки в системе 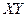, или это уравнение – инвариантно относительно преобразований Галилея.

На основании этого Галилей сформулировал свой принцип относительности:

Физические законы, в различных инерциальных системах отсчета – одинаковы.

До конца 19 века это утверждение не вызывало сомнения.

Уравнение Максвелла, которое описывает электромагнитное явление, не удовлетворяет преобразованиям Галилея. Сомнений в уравнениях Максвелла не было, поэтому возникло предположение неправильности принципа относительности Галилея.

Из уравнения Максвелла следовало, что 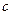(скорость электромагнитных волн (света)) не зависит от выбора системы отсчета, что противоречит преобразованиям Галилея.

Для того, чтобы убедиться, что 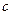не зависит от выбора системы отсчета, рассмотрим эффект Доплера:

Пусть есть источник 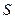, за время 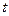, совершает 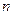- колебаний, которые распространяются в виде волн, со скоростью 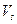, которая не зависит от выбора системы отсчета.

Пусть источник двигается вдоль оси 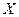со скоростью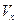

Первое колебание достигнет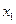

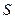
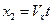
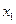
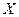
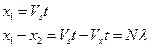
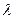- длина волны.

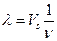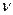; - частота колебаний в системе.

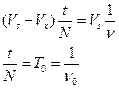
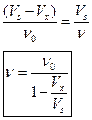
Если источник двигается, то частота меняется.

Если 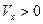- источник приближается, частота растет.

Если 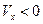- источник удаляется, частота убывает.

Эффект Доплера наблюдается и для электромагнитного излучения.

Тот факт, что электромагнитные волны подчиняются эффекту Доплера, свидетельствует о независимости скорости света.

Опыт Майкельсона и Морли:

зеркало

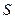
Скорость Земли

Из опыта следует, скорость света не зависит от скорости источника (Земли).

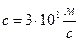
На основании полученных данных, Эйнштейн сформулировал принцип относительности:

1. Физические законы в инерциальных системах отсчета одинаковы

2. Скорость света не зависит от выбора системы отсчета и является максимально возможной скоростью.

Дата добавления: 2014-01-06