Закон сохранения и превращения механической энергии

Закон сохранения энергии в механике представляет собой частный случай всеобщего закона сохранения энергии в природе. В нем речь идет о постоянстве полной энергии. Полной энергией тела в механике называют сумму кинетической и потенциальной энергий данного тела.

Под механической системой подразумевают совокупность материальных тел (точек), рассматриваемых как единое целое.

Силы взаимодействия между материальными телами (точками) механической системы называются внутренними силами.

Силы, с которыми на материальные тела системы действуют внешние (по отношению к данной механической системе) тела, называются внешними силами.

Закон сохранения механической энергии выполняется в изолированной (замкнутой) системе тел. Замкнутой системой тел называется совокупность тел, которые взаимодействуют между собой и не взаимодействуют с другими телами, не принадлежащими этой системе. Замкнутую систему представляет группа астероидов, находящаяся вдали от планет; молекулы газа, сталкивающиеся между собой и со стенками сосуда. Закон сохранения полной механической энергии можно вывести строго математически

Рассмотрим полную механическую энергию некоторой системы, состоящей из n тел массами m₁, m₂, m₃,....., m_n, каждое из которых движется соответственно со скоростями v₁, v₂, v₃,......, v_n.

Уравнение движения каждого из тел имеет следующий вид:

;

…………………….;

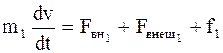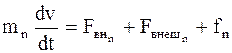, (8.1)

где 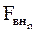- равнодействующие внутренних консервативных сил, действующих на каждую из масс;

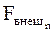- равнодействующие внешних консервативных сил, действующих на каждую из масс;

- равнодействующие внешних неконсервативных сил, действующих на каждую из масс.

Двигаясь под действием сил, тела системы за некоторый промежуток времени dt могут изменить свое положение в системе, совершить некоторые перемещения dr₁, dr₂, dr₃,..., dr_n.

Умножим каждое из уравнений движения скалярно на соответствующее перемещения и, заменив dr_i = vi∙dt, получим

;

;

…………………………………….;

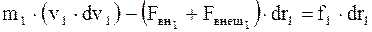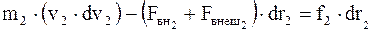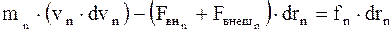. (8.2)

Сложив эти уравнения, будем иметь

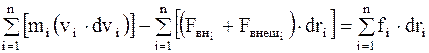, (8.3)

где 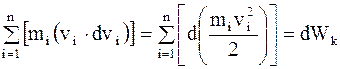- изменение кинетической энергии системы;

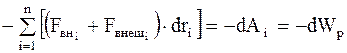- элементарная работа внутренних и внешних консервативных сил, взятая со знаком минус, т.е. изменение потенциальной энергии системы;

- работа внешних неконсервативных сил, действующих на систему.

Таким образом, имеем

d(W_k + W_p) = dA. (8.4)

Следовательно, элементарное изменение полной механической энергии системы при переходе из состояния в состояние равно элементарной работе, совершаемой внешними неконсервативными силами, действующими на систему.

Если внешние неконсервативные силы отсутствуют, то из (8.4) следует, что

d(W_k + W_p) = 0, (8.5)

откуда

W_k + W_p = const, (8.6)

т.е. полная механическая энергия замкнутой системы (в отсутствие внешних воздействий), в которой действуют только консервативные силы, остается величиной постоянной. Данное утверждение и называют законом сохранения механической энергии.

Закон сохранения механической энергии связан с однородностью времени, т.е. инвариантен относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения и не зависят от того, когда тело начало падать.

Системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические), формы, называются диссипативными системами.

Процесс уменьшения механической энергии системы под влиянием внешних факторов называют процессом диссипации (или рассеяния) энергии.

Строго говоря, все системы в природе являются диссипативными.

8.2. Закон сохранения импульса. Центр инерции.
Закон движения центра инерции

Закон сохранения импульса является прямым следствием второго и третьего законов Ньютона.

При этом для изолированного тела он является очевидным следствием второго закона, так как если на тело не действуют никакие силы, то его скорость, а значит, и импульс остаются постоянными. В случае нескольких взаимодействующих между собой, но не подвергающихся воздействию внешних сил, тел (в изолированной системе), этот закон является следствием обоих законов.

Если механическая система состоит из нескольких тел, то согласно третьему закону Ньютона, силы, действующие между этими телами, равны по величине, но противоположны по направлению, а геометрическая сумма внутренних сил равна нулю.

Рассмотрим некоторую систему, состоящую из n тел массами m₁, m₂,..., m_n, каждое из которых движется соответственно со скоростями v₁, v₂,......, v_n.

Уравнение движения каждого из тел имеют вид

;

;

…………………….;

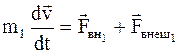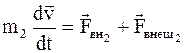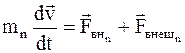, (8.7)

где 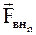- равнодействующие консервативных внутренних сил, действующих на каждую из масс;

- равнодействующие внешних сил, действующих на каждую из масс;

Сложив эти уравнения, получим

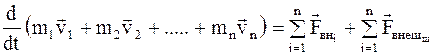(8.8)

или

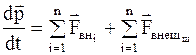, (8.9)

где 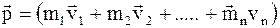- импульс системы;

- равнодействующая всех внутренних сил системы;

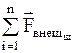- равнодействующая всех внешних сил, действующих на систему.

Так как сумма внутренних сил равна нулю, то

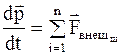. (8.10)

Таким образом, скорость изменения полного импульса замкнутой системы равна геометрической сумме внешних сил, действующих на систему. Следовательно, полный импульс замкнутой системы может изменяться только под действием внешних сил.

В отсутствие внешних сил

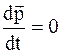, а p = const. (8.11)

Это выражение и является математической формой записи закона сохранения импульса, который утверждает: "Полный импульс замкнутой системы в отсутствие внешних воздействий остается величиной постоянной".

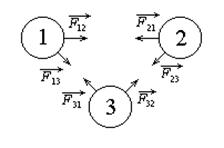Рис.8.1

Докажем справедливость закона сохранения импульса на примере 3-х тел, образующих замкнутую систему (рис.8.1).

В данном случае полный импульс системы

. (8.12)

Возьмем производную по времени

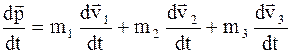. (8.13)

Выражение (8.13) - векторная сумма 3-х сил, действующих на каждое из рассматриваемых тел (второй закон Ньютона). Каждую из указанных сил в свою очередь можно представить в виде векторной суммы сил, действующих на данное тело со стороны двух других тел:

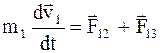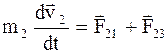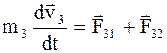; ; . (8.14)

Подставляя (8.14) в (8.13), получим

. (8.15)

В силу третьего закона Ньютона

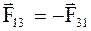; ; . (8.16)

В результате чего сумма сил (8.15) обращается в нуль. Равенство производной нулю означает, что полный импульс системы не зависит от времени, т.е. является постоянной величиной, что и требовалось доказать.

Надо отметить, что реальные системы могут быть замкнутыми только при определенных условиях (в каком-либо направлении), в этом случае можно утверждать, что закон сохранения импульса справедлив только при этих условиях (в данном направлении)

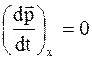, а p _x = const. (8.17)

Закон сохранения импульса справедлив не только в классической физике. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц, взаимодействия между которыми подчиняются законам квантовой механики. Этот закон универсален, является одним из фундаментальных законов природы и следствием определенного свойства симметрии пространства - его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора места положения начала координат инерциальной системы отсчета.

Надо отметить, что импульс незамкнутой системы также сохраняется, если геометрическая сумма всех внешних сил равна нулю.

В классической механике из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс.

Центром масс (или центром инерции) системы называется воображаемая точка С, положение которой характеризует распределение массы этой системы, которая определяется радиус-вектором

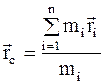, (8.18)

где m_i и r_i - соответственно масса и радиус-вектор i-й материальной точки;

n - число материальных точек в системе.

Скорость центра масс

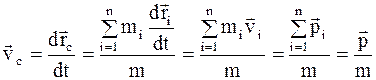, (8.19)

где 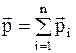- полный импульс системы.

Из (8.19) можно написать

p = m v _c, (8.20)

т.е. полный импульс системы равен произведению массы системы на скорость ее центра масс.

Подставив (8.20) в уравнение (8.10), получим

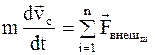. (8.21)

Таким образом, центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует равнодействующая всех внешних сил (уравнение движения центра масс и воображаемой материальной точки имеют один и тот же вид).

Выражение (8.21) представляет собой закон движения центра масс.

В соответствии с (8.21) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.

8.3. Закон сохранения момента импульса. Уравнение моментов

Известно, что моментом импульса (моментом количества движения) материальной точки называется векторная физическая величина, численно равная произведению ее импульса (количества движения) на плечо, т.е. на кратчайшее расстояние от направления импульса до оси (или центра) вращения:

L_i = m_iv_ir_i = m_iω_ir_i×r_i= m_ir_i²×ω_i = I_iω, (8.22)

где I_i - момент инерции материальной точки относительно выбранной оси (выбранного центра) вращения;

ω - угловая скорость материальной точки.

Дата добавления: 2014-01-06