В векторной форме

L_i = I_i× ω или L = [ r ´ p ]. (8.23)

Момент импульса твердого тела (системы) относительно выбранной оси (или центра) вращения равен сумме моментов импульса отдельно взятых материальных точек тела (тел системы) относительно той же оси (того же центра) вращения. При этом

L = I ω, (8.24)

где - момент инерции тела (системы);

ω - угловая скорость.

Основное уравнение динамики вращательного движения материальной точки имеет вид

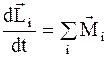, (8.25)

где L_i - момент импульса материальной точки относительно начала координат;

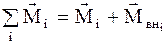- суммарный вращающий момент, действующий на i-ю материальную точку;

- результирующий момент всех внутренних сил, действующих на материальную точку;

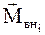- результирующий момент всех внешних сил, действующих на материальную точку.

Для тела, состоящего из n материальных точек (системы из n тел):

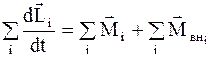. (8.26)

Так как 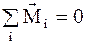- момент всех внутренних сил равен нулю, то

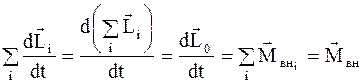или 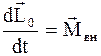, (8.27)

где L ₀ - момент импульса тела (системы) относительно начала координат;

M _вн - суммарный вращающий момент внешних сил, действующих на тело (систему).

Из (8.27) следует, что момент импульса тела (системы) может изменяться под действием момента внешних сил, а скорость его изменения равна суммарному вращающему моменту внешних сил, действующих на тело (систему).

Если M_вн = 0, то

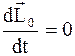, а L ₀ = const. (8.28)

Таким образом, если на тело (замкнутую систему) не действует внешний вращающий момент, то его момент импульса остается величиной постоянной. Данное утверждение и называют законом сохранения момента импульса.

Для реальных систем закон сохранения момента импульса можно записать так

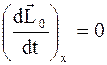, а (L ₀)_x = const. (8.29)

Из закона сохранения момента импульса следует: если тело не вращалось

(ω = 0), то при M = 0 оно и не придет во вращение; если тело совершало вращательное движение, то при M = 0, оно будет совершать равномерное вращательное движение.

Уравнения 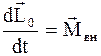, 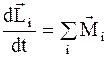называют уравнениями моментов, соответственно для тела (системы) или материальной точки.

Уравнение моментов указывает, как изменяется момент импульса под действием сил. Так как d L ₀ = M ∙dt, то момент сил, совпадающий по направлению с моментом импульса, увеличивает его. Если же момент сил направлен навстречу моменту импульса, то последний уменьшается.

Уравнение моментов справедливо для любой произвольно выбранной неподвижной оси вращения.

Приведем несколько примеров:

а ) когда кошка неожиданно для себя падает с большой высоты, она усиленно вращает хвостом в ту или иную сторону, добиваясь оптимального разворота своего тела для благоприятного приземления;

б ) человек перемещается по краю круглой, свободно вращающейся платформы: пусть моменты импульса платформы и человека соответственно равны 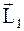и 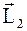, тогда, принимая систему замкнутой, получим

, , .

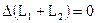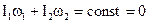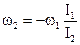Т.е. угловые скорости вращения этих тел вокруг их общей оси будут обратны по знаку, а по величине – обратно пропорциональны их моментам инерции;

в ) опыт со скамьей Жуковского. Человек, находящийся посередине скамьи и вращающийся вместе с платформой, притягивает к себе грузы. Пренебрегая трением в опорных подшипниках, считаем момент силы равным нулю:

, , .

, .

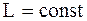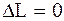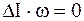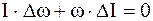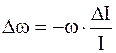При 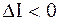, , 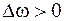если же 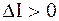, то ;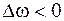

г)при фигурном катании на коньках спортсмен, выполняя вращение, складывается и при этом ускоряет свое вращение;

д ) гироскопы - устройства, принцип действия которых основан на законе сохранения момента импульса тела: 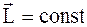. Предназначены для фиксирования первоначально заданного направления в пространстве на объекте, который перемещается в произвольном направлении и неравномерно (космические ракеты, танки и др.).

8.4. Применение законов сохранения к упругому и неупругому взаимодействиям (удару)

Удар - совокупность явлений, возникающих при столкновении движущихся твердых тел, а также при некоторых видах взаимодействия твердого тела с жидкостью или газом (удар струи о тело, удар тела с поверхностью жидкости, гидравлический удар, действие взрывной или ударной волны на твердое тело и др.).

Промежуток времени, в течение которого длится удар (время удара), обычно очень мал (на практике ~ 10^-4 – 10^-5 с), а развивающиеся на площадках контакта соударяющихся тел силы (так называемые ударные или мгновенные) очень велики. За время удара они изменяются в широких пределах и достигают значений, при которых средние величины давления (напряжений) на площадках контакта имеют порядок 10⁹ и даже 10¹⁰ Па. Действие ударных сил за время удара приводит к значительному изменению скоростей точек тела.

Следствиями удара могут быть также остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств материалов (в частности, их упрочнение), полиморфные и химические превращения, а при скоростях соударения, превышающих критические, - разрушение тел в месте удара. Критические скорости для металлов имеют порядок 15 м/с (медь) - 150 м/с и более (высококачественные стали).

Изменение скорости точек тела за время удара определяется методами общей теории удара, где в качестве меры механического взаимодействия тел при ударе вместо самой ударной силы F вводится ее импульс за время удара τ, т.е. величина, которую называют ударным импульсом:

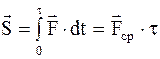. (8.30)

Одновременно ввиду малости t импульсами всех неударных сил, таких, например, как сила тяжести, а также перемещениями точек тела за время удара пренебрегают.

Основные уравнения общей теории удара вытекают из теорем (законов) об изменении количества движения и кинетического момента системы. С помощью этих теорем, зная приложенный ударный импульс и скорости в начале удара, определяют скорости в конце удара, а если тело является несвободным, то и импульсивные реакции связей.

Процесс соударения двух тел можно разделить на две фазы. Первая фаза начинается с момента соприкосновения точек А и В тел, имеющих в этот момент скорость сближения (v_An – v_Bn), где v_An и v_Bn проекции скоростей v_A и v_B на обшую нормаль n к поверхности тел в точках А и В, называемой линией удара. К концу первой фазы сближение тел прекращается, а часть их кинетической энергии переходит в потенциальную энергию деформации. Во второй фазе происходит обратный переход потенциальной энергии упругой деформации в кинетическую энергию тел. При этом тела начинают расходиться, и к концу второй фазы точки А и В будут иметь скорость расхождения (u_An – u_Bn).

Для абсолютно упругих тел механическая энергия к концу удара восстановливается полностью и выполняется соотношение

çv_An – v_Bnç = çu_An – u_Bnç. (8.31)

При взаимодействии абсолютно неупругих тел удар заканчивается на первой фазе и выполняется соотношение

u_An – u_Bn = 0. (8.32)

В случае удара реальных тел механическая энергия к концу удара восстанавливается лишь частично вследствие различных потерь (образование остаточных деформаций, нагревание), при этом

çu_An – u_Bnç<çv_An – v_Bnç. (8.33)

Для учета этих потерь вводится в рассмотрение так называемый коэффициент восстановления k, который считается зависящим только от физических свойств материалов взаимодействующих тел, численно равный отношению скоростей удаления тел после взаимодействия к скорости их сближения:

. (8.34)

В случае удара по неподвижному телу u_An = v_Bn = 0 и

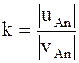. (8.35)

Коэффициент восстановления определяется экспериментально (при соударении тел из дерева k ~ 0,5; из стали - k ~ 0,55; слоновой кости - k ~ 0,89; стекла - k ~ 0,94; в предельных случаях при абсолютно упругом ударе - k = 1; при абсолютно неупругом - k = 0).

Зная скорости в начале удара и коэффициент восстановления, можно найти скорости в конце удара и действующий в точках соударения ударный импульс.

Если центры масс тел С₁ и С₂ лежат на линии удара, то удар называют центральным; в противном случае - нецентральным. Если скорости v₁ и v₂ центров масс в начале удара направлены параллельно линии удара, то удар называется прямым; в противном случае - косым.

Можно показать, что при прямом центральном ударе двух гладких тел (шаров) 1 и 2

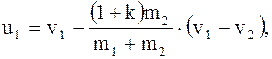(8.36)

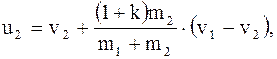(8.37)

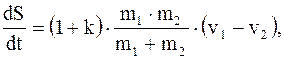(8.38)

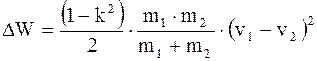, (8.39)

где DW - потерянная за время удара кинетическая энергия системы;

m₁, m₂ - массы тел.

Из выражений (8.36, 8.37) в частном случае при k = 1 и m₁ = m₂ получается

u₁ = v₂; u₂ = v₁, (8.40)

т.е. тела одинаковой массы при абсолютно упругом ударе обмениваются скоростями; при этом DW = 0.

Для определения времени удара, ударных сил и вызванных ими в телах напряжений и деформаций необходимо учесть механические свойства материалов тел и изменения этих свойств за время удара, а также характер начальных и граничных условий. Решение проблемы существенно усложняется не только из-за трудностей чисто математического характера, но и ввиду отсутствия достаточных данных о параметрах, определяющих поведение материалов тел при ударных нагрузках, что заставляет делать при расчетах ряд существенных упрощающих предположений.

Наиболее разработана теория удара абсолютно упругих тел, в которой предполагается, что тела за время удара подчиняются законам упругого деформирования (теории упругости) и в них не появляется остаточных деформаций. Деформация, возникающая в месте контакта, распространяется в таком теле в виде упругих волн со скоростью, зависящей от физических свойств материала.

Если время прохождения этих волн через все тело много меньше времени удара, то влиянием упругих колебаний можно пренебречь и считать характер контактных взаимодействий при ударе таким же, как в статическом состоянии. На таких допущениях основывается контактная теория удара Г. Герца.

Если же время прохождения упругих волн через тело сравнимо со временем удара, то для расчетов пользуются волновой теорией удара.

Изучение удара не вполне упругих тел - задача значительно более сложная, требующая учета как упругих, так и пластических свойств материалов. При решении этой задачи и связанных с ней проблем определения механических свойств материалов тел при ударе, изучения изменений их структуры и процессов разрушения широко опираются на анализ и обобщение результатов многочисленных экспериментальных исследований.

Экспериментально исследуются также специфические особенности удара тел при больших скоростях (порядка сотен м/с) и при воздействии взрыва, который в случае непосредственного контакта заряда с телом можно считать эквивалентным соударению со скоростью до 1000 м/с.

Кроме удара твердых тел, в физике изучают столкновения молекул, атомов, элементарных частиц.

Дата добавления: 2014-01-06