Цифровые фильтры

Функциональная схема цифрового фильтра. В отличие от дискретных фильтров в цифровом фильтре (ЦФ) осуществляется обработка цифровых сигналов (рис. 19.1, в). На рис. 19.60 изображена функциональная схема цифровой обработки аналоговых сигналов. Аналоговый сигнал x (t) подается на аналого-цифровой преобразователь (АЦП), где осуществляется дискретизация, квантование непрерывного сигнала и его кодирование. В результате на выходе АЦП формируется цифровой сигнал, представляющий собой последовательность двоичных чисел с фиксированным количеством разрядов.

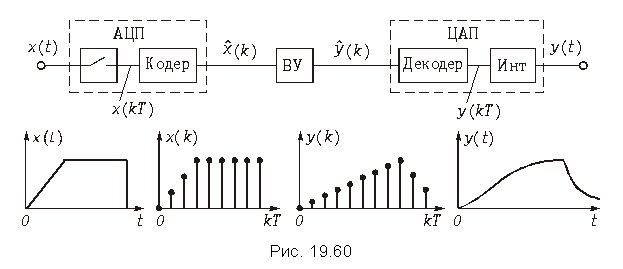
Например, если отсчет имеет величину 30 В, то запись числа в двоичном 8-разрядном коде будет такой: 00011110. Закодированные в двоичном коде отсчеты на выходе кодера АЦП на рисунке обозначены . Далее двоичная последовательность поступает на вычислительное устройство (ВУ), которое представляет собой универсальную или специализированную микро ЭВМ, микропроцессорное или любое другое вычислительное устройство. Главное состоит в том, что в памяти ВУ должна быть записана программа вычисления, например, выражение (19.35), и отсчеты импульсной реакции, заданной цепи. Следовательно, в результате работы программы ВУ будет выдавать закодированные в двоичном коде отсчеты 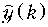. Далее двоичная выходная последовательность поступает на вход цифро-аналогового преобразователя (ЦАП), содержащий декодер и интерполятор. В ЦАП осуществляется декодирование сигнала, в результате формируется дискретный выходной сигнал y (kT) и после интерполяции на выходе ЦАП получаем выходной аналоговый сигнал y (t).

Как видим, ВУ может сыграть роль реальной цепи. И хотя самой физической цепи в наличии может и не быть, а задана она будет лишь в виде отсчетов импульсной реакции и программы вычислений, мы будет наблюдать на выходе описанной системы такое же выходное напряжение y (t), как и на выходе реальной цепи.

Следует отметить, что при цифровой обработке ЦАП может и отсутствовать, если выходной сигнал надо получить в цифровой форме.

Аналогово-цифровое преобразование сигналов. Как следует из рис. 19.60 АЦП осуществляет дискретизацию аналогового сигнала, его квантование по уровню с шагом D (рис. 19.1, в) и кодирование. Обычно процесс квантования осуществляется одновременно с его кодированием, в результате на выходе АЦП получаем сигнал, представленный в некотором цифровом коде.

Одним из основных параметров кода является его основание, соответствующее выбранной системе счисления. Близко к оптимальным реализуются двоичные или бинарные коды, которые нашли наибольшее распространение в связи.

Известно большое количество различных устройств преобразования непрерывного сообщения в бинарный код. Все их можно разбить на три основные группы: преобразователи последовательного счета, поразрядного кодирования и преобразователи считывания. Наибольшее применение в связи нашли преобразователи первых двух типов.

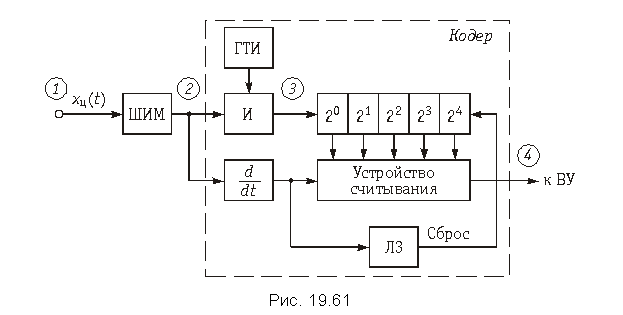
Принцип действия преобразователя последовательного счета с временным преобразованием иллюстрируется схемой изображенной на рис. 19.61 и временными диаграммами на рис. 19.62.

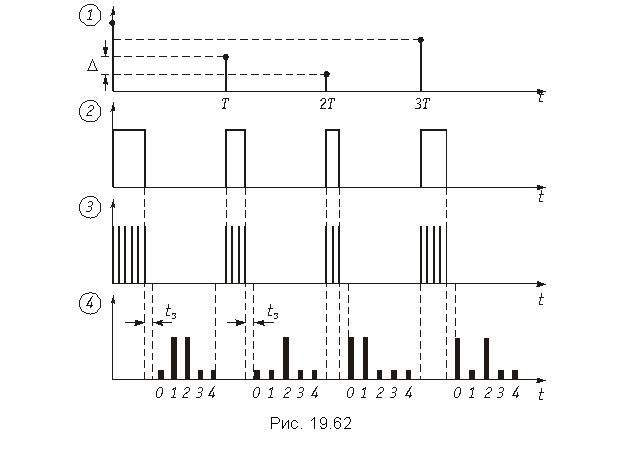
Кодирование в данной схеме осуществляется следующим образом. Аналоговый сигнал после дискретизации и квантования x _ц(t) поступает на вход широтно-импульсного модулятора (ШИМ), на выходе которого формируются прямоугольные импульсы ширина которых пропорциональна отсчету сигнала x _ц(t) в моменты kT (рис. 19.62). Далее этот ШИМ-сигнал подается на схему «И», на второй вход которой поступают импульсы с генератора тактовой частоты (ГТИ). На выходе схемы «И» формируются импульсы, число которых в «пачке» пропорционально ширине импульса. Эти импульсы поступают в двоичный счетчик, где число их фиксируется в двоичной системе счисления. Задним фронтом ШИМ-импуль­са запускается устройство считывания результата, с выхода которого кодовая комбинация поступает в ВУ. Считывание может осуществляться последовательно или параллельно (последовательный или параллельный код).

На рис. 19.62 приведен вид кодовой группы на выходе при последовательном считывании. Для возвращения двоичного счетчика в исходное состояние на него через линию задержки ЛЗ с t_з = t_счит подается сигнал сброса, формируемый задним фронтом ШИМ-им­пульса. С приходом следующего измерительного импульса работа кодера повторяется.

Аналогичным образом можно кодировать и амплитудно-модули­ро­ванную импульсную последовательность (кодер последовательного счета с частотным преобразованием). Для этого АИМ-сигнал подается на ЧМ-генератор (мультивибратор), и осуществляется счет импульсов этого генератора за фиксированные промежутки времени по рассмотренной выше схеме.

В преобразователях поразрядного кодирования производится последовательное сравнение выходного сигнала с набором эталонных напряжений, каждое из которых соответствует определенному разряду кода. В качестве эталонных напряжений используется геометрическая прогрессия вида

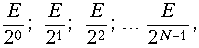
где N – число разрядов в бинарном коде. Причем E > u_max, где u_max – максимально возможное значение кодирующего сигнала.

При поразрядном кодировании вначале формируется старший разряд кода путем сравнения u (t) с 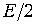(например, если 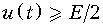, то формируется символ «1», в противном случае – «0»). Одновременно на выходе схемы сравнения образуется напряжение 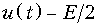при 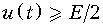или u (t) при 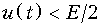. Затем указанная процедура повторяется с полученным напряжением для эталонного напряжения 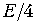и т. д. В результате N сравнений получается символ самого младшего разряда.

Шумы квантования. При квантовании сигнала минимальный шаг квантования D (расстояние между смежными разрешенными уровнями) соответствует единице младшего двоичного разряда. Причем, поскольку при квантовании происходит округление значений сигнала до ближайшего дискретного уровня, то появляются ошибки округления . Если x (t) известен неточно, то e – является случайной величиной и при малом D распределено по равномерному закону. Последовательность значений ошибки e, возникающей при квантовании дискретного сигнала x (kT) образует дискретный случайный процесс e(kT) называемый шумом квантования (рис. 19.63).

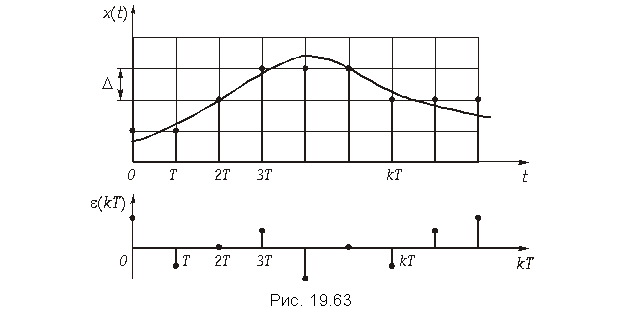
Дисперсия шума квантования определяется для равномерного закона распределения p (e) формулой

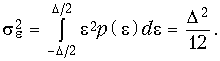(19.58)

Если шаг квантования D мал, то соседние значения e(kT) можно считать некоррелированными.

Шум квантования является одним из главных источников погрешности цифровой обработки сигнала. Шум на выходе цифрового фильтра x(kT) при условии некоррелированности отсчетов e(kT) можно определить согласно (19.35)

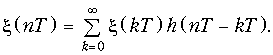(19.59)

Откуда с учетом (19.59) получим для дисперсии шума на выходе цифрового фильтра:

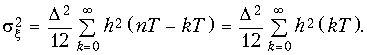(19.60)

Поскольку для ЦФ обычно выполняется условие (19.36),то дисперсия шума квантования на выходе всегда конечна.

Ошибки округления. При обработке цифрового сигнала в ВУ возникают дополнительные ошибки округления (усечения). Действительно, если при использовании в ВУ чисел с фиксированной запятой сложение чисел не приводит к увеличению разрядов, то при умножении число разрядов возрастает и возникает необходи
мость округления результата, что естественно приводит к ошибкам называемым ошибками округления. По своему характеру эти ошибки аналогичны шуму квантования. Для их учета обычно в схему ЦФ дополнительно вводят источники шума e_i (kT), число которых равно числу умножителей. На рис. 19.64 изображена схема рекурсивного ЦФ звена 1-го порядка с учетом источников шума округления.

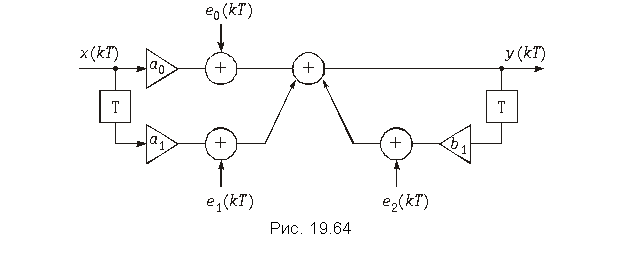
Источники шума e (kT) имеют одинаковую дисперсию s² = 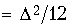, где D определяется числом используемых разрядов. Если принять, что источники e ₀(kT), e ₁(kT) и e ₂(kT) независимы, то дисперсия суммарного шума округления будет равна

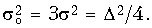
Для другой схемы реализации ЦФ результирующая 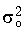вычисляется в зависимости от того, куда будет подключен источник шума e (kT) и в общем случае может быть найден по формуле (19.60) или с учетом равенства Парсеваля

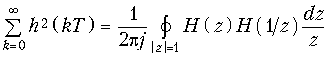(19.61)

из уравнения

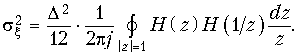(19.62)

Пример. Определить дисперсию шума на выходе 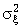ЦФ 1-го порядка с передаточной функцией

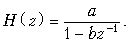
Для нахождения 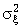воспользуемся формулой (19.62):

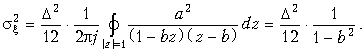
Кроме ошибок квантования и округления при синтезе ЦФ возникают ошибки, вызванные неточными значениями параметров фильтра. Эти ошибки особенно опасны в рекурсивных фильтрах высокого порядка, т. к. могут привести к потере устойчивости ЦФ, поэтому обычно используют звенья 1-го и 2-го порядков (см. § 19.5). Кроме рассмотренных выше при синтезе ЦФ возникают еще ряд дополнительных явлений, приводящих к погрешности цифровой фильтрации. К ним, например, относятся так называемые предельные циклы низкого уровня, представляющие собой периодические колебания, возникающие на выходе ЦФ при низком входном сигнале и обусловленные округлением результатов вычисления. Все эти явления и ошибки подробно исследуются в специальной литературе.

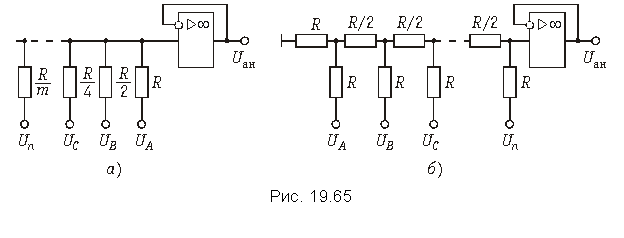
Цифро-аналоговое преобразование. Преобразование цифровых сигналов в аналоговый осуществляется с помощью различных цифро-аналоговых преобразователей (ЦАП). В основе простейшего ЦАП лежит принцип двоично-взвешенного суммирования напряжений или токов. На рис. 19.65 изображены схемы простейших ЦАП на базе резистивных цепей.

В ЦАП с двоично-весовыми резисторами (рис. 19.65, а) требуется меньшее число резисторов, однако при этом необходим целый ряд номиналов прецизионных сопротивлений. Аналоговое выходное напряжение U _ан ЦАП определяется как функция двухуровневых входных напряжений:

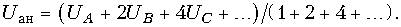
На цифровых входах U_А, U_В, U_С... напряжение может принимать лишь два фиксированных значения, например, либо 0, либо 1.

Для ЦАП, в котором используются резисторы R и 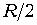, требуется больше резисторов (рис. 19.65, б), но только с двумя номиналами. Аналоговое напряжение на выходе такого ЦАП определяется по формуле

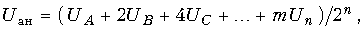
где n – число разрядов ЦАП; m – коэффициент, зависящий от числа разрядов ЦАП.

Для обеспечения высокой точности работы резистивные цепи ЦАП должны работать на высокоомную нагрузку. Чтобы согласовать резистивные цепи с низкоомной нагрузкой, используют буферные усилители на основе операционных усилителей, показанные на рис. 19.65, а, б.

Интерполяторы. На выходе ЦАП сигнал обычно имеет форму последовательности импульсов модулированных по амплитуде (АИМ-сигнал). Для восстановления (демодуляции) из АИМ-после­до­вательности аналогового сигнала достаточно использовать ФНЧ с частотой среза w_с = 2p/ Т, где Т – частота дискретизации АИМ-сигнала. Существуют и более сложные интерполирующие устройства, которые описаны в специальной литературе.

В заключении следует отметить, что в связи с бурным развитием вычислительной, микропроцессорной техники цифровые методы обработки сигналов получают все большее распространение. Они имеют более широкие возможности реализации сложных и эффективных алгоритмов обработки сигналов, которые в большинстве своем недоступны для реализации аналоговыми цепями.

Вопросы и задания для самопроверки

1. Почему нельзя произвольно выбирать интервал дискретизации?

2. Найдите спектр дискретного сигнала, состоящего из одного отсчета x { k } = {2}.

3. Каким должно быть соотношение между интервалом дискретизации спектра по частоте D F и периодом повторения Т _с сигнала?

4. Найдите частоту дискретизации и интервал дискретизации сигнала, имеющего спектр, ограниченный частотой F _в = 10 кГц.

5. Найти дискретную свертку сигналов x ₁{ k } = {1; 1} и x ₂{ k } = {0,5; 0,5; 0,5}.

Ответ: x ₁{ k } * x ₂{ k } = {0,5; 1; 1; 0,5}.

6. Вычислить реакцию дискретной цепи с импульсной характеристикой h (k) на входной дискретный сигнал x (k):

а) h { k } = {2; 1; 0,5}, x { k } = {0,5; 0,5}

б) h { k } = {2; 2; 2}, x { k } = {1; 1; 1}.

Ответ: а) y { k } = {1; 1,5; 0,75; 0,25}

б) y { k } = {2; 4; 6; 4; 2}.

7. Найти z -преобразование дискретных сигналов

а) 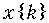= {3; 2; 1}

б)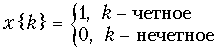

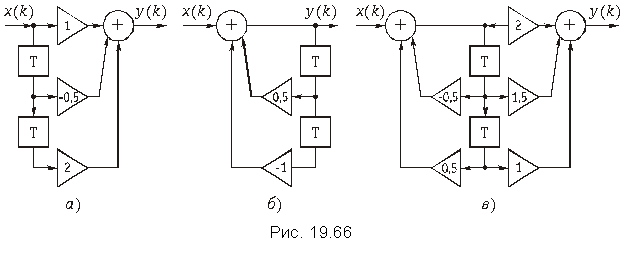
в) .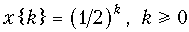

Ответ: а)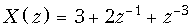

б)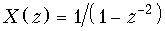

в) .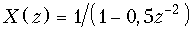

8. Найти z -преобразование дискретного сигнала x ₃(k), равного сумме сигналов x ₁{ k } = {1; 0; 1; –1} и x ₂{ k } = {2; 1; 0; 1}

Ответ: .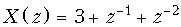

9. Найти дискретные сигналы x (k), имеющие z -преобразования

а)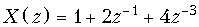

б) .

Ответ: а) x { k } = {1; 2; 0; 4}

б) x { k } .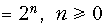

10. Найти ДПФ дискретного сигнала x { k } = {0,5; 0,25; 0,0625}. Построить спектр амплитуд и спектр фаз дискретного сигнала.

Ответ: X { n } = {1,875; 0,838; 0,625; 0,838}

arg X { n } = {0; –0,464; 0,0464}.

11. Найти отсчеты дискретных сигналов x (k), имеющих спектры

а) X { n } = {4; 0; 0; 0}

б) X { n } = {0; 4; 0; 0}.

Ответ: а) x { k } = {1; 1; 1; 1}

б) 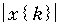= {1; 1; 1; 1}, .

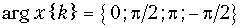12. Записать разностные уравнения для дискретных цепей, струк­турные схемы которых приведены на рис. 19.66.

Ответ: а)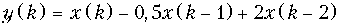

б)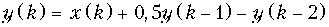

в)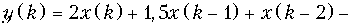

.

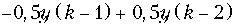13. Записать передаточные функции цепей, приведенных на рис. 19.66, и определить их импульсные характеристики.

Ответ: а) 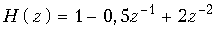, h { k } = {1; –0,5; 2}

б) ,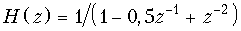

h { k } = {1; 0,5; –0,75; –0,875;...}

в) 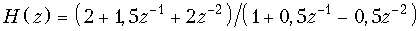, h { k } = {2; 0,5; 1,75; –0,625;...}.

14. Рассчитать отсчеты y (0), y (1) и y (2) выходных сигналов цепей, приведенных на рис. 19.66, если входной сигнал – ступенчатая последовательность x { k } = u { k } = {1; 1; 1; 1;...}.

Ответ: а) y { k } = {1; 0,5; 2,5}

б) y { k } = {1; 1,5; 0,75}

в) y { k } = {2; 2,5; 4,25}.

15. Определить импульсные характеристики цепей, описываемых разностными уравнениями:

а)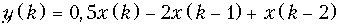

б)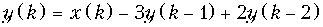

в) .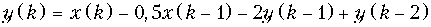

Ответ: а) h { k } = {0,5; –2; 1}

б) h { k } = {1; –3; 11; –39;...}

в) h { k } = {1; –2,5; 6; –14,5;...}.

16. Определить передаточные функции цепей, описываемых разностными уравнениями, приведенными в задаче 15.

Ответ: а)

б)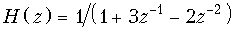

в) .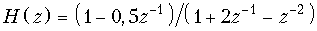

17. Составить структурные схемы, записать разностные уравнения и определить импульсные характеристики цепей, передаточные функции которых имеют вид

а)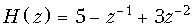

б)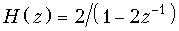

в) .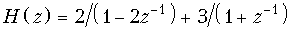

Ответ: а) ,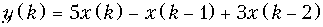

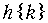= {5; –1; 3}

б) ,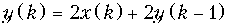

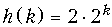= {2; 4; 8; 16;...}

в) ,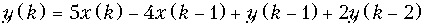

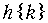= {5; 1; 11; 13;...}.

18. Определить устойчивость цепей, имеющих передаточные функ­ции, приведенные в задаче 17.

Ответ: а) устойчивая

б) неустойчивая

в) неустойчивая.

19. Определить передаточную функцию цепи, если на ее входе и выходе действуют дискретные сигналы x { k } = {1; 0; 0; 0; 1; 0; 0; 0; 1;...}, y { k } = {1; 0; 1; 0; 1; 0;...}.

Ответ: .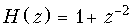

20. Найти импульсные характеристики дискретных цепей, имеющих передаточные функции

а)

б)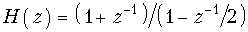

Составить структурную схему каскадного соединения этих цепей, определить для нее передаточную функцию и записать разностное уравнение.

Ответ: а) 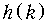= 1, k 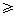0

б)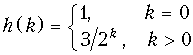

.

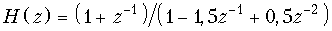
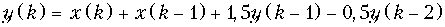21. Найти передаточную функцию дискретной цепи с импульсной характеристикой

а) 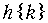= {1; –1}

б) .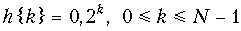

Ответ: а)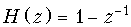

б) .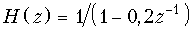

22. Определить сигнал на выходе дискретной цепи с импульсной характеристикой h { k } = {1; 0,5}, если на вход подается сигнал x { k } = {1; 1; 1}.

Ответ: y { k } = {1; 1,5; 1,5; 0,5}.

23. Определить передаточные функции и АЧХ дискретных цепей, имеющих разностные уравнения:

а)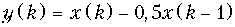

б) .

Ответ: а)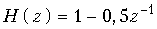

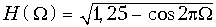
б)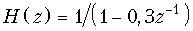

.

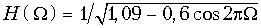24. Вычислить дисперсию шума на выходе ЦФ первого порядка с передаточной функцией 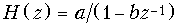; (b < 1) с использованием формулы (19.60).

Ответ: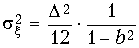

ГЛАВА 18. КОРРЕКТИРУЮЩИЕ ЦЕПИ И ИХ СИНТЕЗ

Дата добавления: 2014-01-06