Принцип корректирования искажений

Корректирование амплитудно-частотных искажений. Рассмотрим некоторую электрическую цепь – четырехполюсник (рис. 18.1), имеющую амплитудно-частотную характеристику (АЧХ), изобра-женную на рис. 18.2, а, а ослабление – на рис. 18.2, б. Пусть для упрощения входной сигнал состоит из суммы всего двух гармоник с частотами w₁ и 2w₁ (рис. 18.3, а). Форма входного сигнала показана на этом рисунке жирной линией.
Из анализа графиков АЧХ и ослабления цепи следует, что ам-плитуда первой гармоники при прохождении сигнала через цепь останется практически неизменной, а амплитуда второй гармоники уменьшится в несколько раз.

Результат сложения гармоник на выходе цепи дает форму сигнала, отличающуюся от входной (рис. 18.3, б).

Изменение формы сигнала на выходе цепи по сравнению с формой сигнала на ее входе называется искажением сигнала. Когда искажения формы сигнала связаны с непостоянством амплитудно-частотной характеристики цепи, они носят название амплитудно-частотных искажений.

Таким образом, условием отсутствия амплитудно-частотных искажений в цепи следует считать постоянство ее АЧХ (ослабления) на всех частотах (см. § 9.9):

На практике условие (18.1) часто не выполняется, т. е. АЧХ и ослабление цепей аппаратуры и линий связи не являются постоянными. Эти цепи практически всегда вносят амплитудно-частотные искажения в передаваемый сигнал. Устранить подобные искажения полностью не удается, но их можно уменьшить до величин, допустимых соответствующими нормами. Для этих цепей применяются амплитудные корректоры.

Амплитудный корректор - это четырехполюсник, который включается каскадно с цепью. Его задача заключается в том, чтоб

дополнить АЧХ цепи или ее рабочее ослабление до постоянной величины на всех частотах рабочего диапазона. Вне рабочего диапазона АЧХ цепи может иметь любую форму.

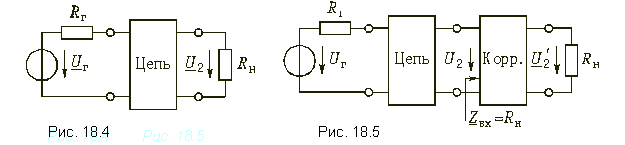
На рис. 18.4 изображена цепь, работающая между генератором с внутренним сопротивлением Rг и нагрузкой Rн. Рабочий коэффициент передачи этой цепи в соответствии с (12.44) равен:

Для достижения условий безискаженной передачи между цепью и нагрузкой включен корректор (рис. 18.5). Чтобы режим работы цепи не нарушался, входное сопротивление корректора должно равняться сопротивлению нагрузки. Очевидно, только при этом условии напряжение на выходе цепи будет равно U2, как и в схеме рис. 18.4 до включения корректора.

Если обозначить напряжение на выходе каскадного соединения цепи и корректора U2¢, то рабочий коэффициент передачи такого соединения запишется в виде

Разделим и умножим это выражение на U2 и представим его в виде произведения двух сомножителей

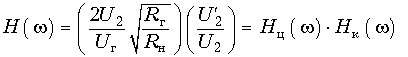
Первый сомножитель представляет рабочий коэффициент передачи цепи (см. рис. 18.4), а второй - коэффициент передачи по напряжению корректора.

Ослабление, вносимое каскадным соединением цепи и корректора,

вычисляется путем сложения ослаблений цепи и корректора.

Из рис. 18.6 видно, что корректор должен вносить ослабление, дополняющее ослабление цепи в рабочей полосе частот wн ё wв до постоянной величины А0.

Корректирование фазочастотных искажений. Рассмотрим электрическую цепь - четырехполюсник (рис. 18.7), имеющую рабочую фазовую постоянную B(w), изображенную на рис. 18.8, а, и характеристику группового времени прохождения (ГВП) tгр(w), являющуюся производной от рабочей фазовой постоянной, - на рис. 18.8, б. Входной сигнал uвх(t) состоит из суммы двух гармоник с частотами w1 и 2w1 (рис. 18.9, а). Форма входного сигнала изображена на этом рисунке жирной линией.

Анализ графиков B(w) и tгр(w) цепи показывает, что фаза первой гармоники почти не меняется при прохождении сигнала через цепь, а фаза второй гармоники существенно увеличивается.

В результате сложения гармоник на выходе цепи получается сигнал, форма которого отличается от входной (рис. 18.9, б).

Искажения формы сигнала при прохождении его по цепи, обусловленные нелинейностью фазо-частотной характеристики цепи или непостоянством группового времени прохождения, называются фазо-частотными искажениями.

Условием отсутствия фазо-частотных искажений в цепи следует считать линейность рабочей фазовой постоянной B(w) и ФЧХ цепи (рис. 18.10, а):

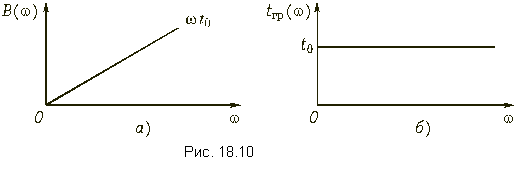
Производная от фазо-частотной характеристики - это групповое время прохождения, которое для неискажающей цепи:

должна быть постоянной на всех частотах (рис. 18.10, б).

В реальных цепях условия (18.2) и (18.3) обычно не выполняются, т. е. ФЧХ не является линейной, а ГВП - не постоянно. Такие цепи вносят фазо-частотные искажения в передаваемый сигнал. Для уменьшения подобных искажений до допустимых значений применяют фазовые корректоры.

Фазовый корректор - это четырехполюсник, включаемый каскадно с цепью и дополняющий фазовую характеристику цепи до линейной. Вместо корректирования частотной характеристики фазы можно выравнивать характеристику группового времени прохождения так, чтобы она была постоянной на всех частотах рабочего диапазона. Фазовый корректор не должен искажать АЧХ цепи.

На рис. 18.11 для достижения условий безискаженной передачи между генератором и нагрузкой включено каскадное соединение цепи с ФЧХ, подлежащей коррекции, и корректора. Входное сопротивление фазового корректора должно равняться сопротивлению нагрузки, чтобы условия работы цепи не изменялись по сравнению с теми, в которых находится цепь, включенная между генератором и нагрузкой в отсутствие корректора.

Передаточная функция цепи, изображенной на рис. 18.11:

Умножим и разделим это выражение на U2 и представим его в виде произведения передаточных функций цепи Hц(jw) и корректора Hк(jw):

Фазо-частотная характеристика каскадного соединения цепи и корректора:

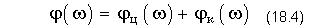
вычисляется как сумма ФЧХ цепи и корректора.

Из рис. 18.12 видно, что фазовый корректор должен дополнять ФЧХ цепи в рабочей полосе частот wн ё wв до линейной зависимости (рис. 18.12, а) либо дополнять групповое время прохождения цепи до постоянной величины t0 в том же рабочем диапазоне частот (рис. 18.12, б). За пределами рабочего диапазона ФЧХ и ГВП могут иметь любую форму.

Корректоры бывают постоянными и непостоянными (регулируемыми). Характеристики постоянных корректоров не меняются при изменении характеристик цепи. Существуют корректоры, характеристики которых можно изменить в зависимости от изменения параметров цепи. Изменение параметров цепи возможно, во-первых, при изменении показателей окружающей среды, прежде всего температуры. Во-вторых, в технике связи распространены коммутируемые сети, когда канал связи между двумя пользователями устанавливается случайным образом на время сеанса связи и заранее неизвестно, из каких участков он будет составлен. Погрешности в АЧХ и ФЧХ, вносимые каждым участком могут складываться неудачно, так что общая погрешность будет больше допустимых величин. В этом случае включают так называемые "подчисточные" корректоры. Настройку регулируемых корректоров производят либо вручную, либо автоматически.

Дата добавления: 2014-01-06