
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы, основанные на алгебраическом интерполировании
|
|
|
|
Рассмотрим уравнение (4.1). Пусть 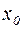 - некоторое приближение к его решению. Разложим левую часть уравнения по формуле Тейлора в точке
- некоторое приближение к его решению. Разложим левую часть уравнения по формуле Тейлора в точке 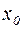
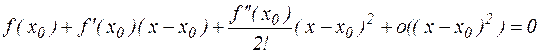 . (4.2)
. (4.2)
Метод Ньютона. Ограничимся в разложении (4.2) первыми двумя слагаемыми
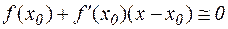
и разрешим полученное выражение относительно х
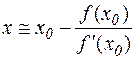 .
.
Последнее соотношение принимается в качестве базового для формирования вычислительного процесса. Он описывается формулой

| (4.3) |
и называется методом Ньютона. Заметим, что правило (4.3) имеет вполне определённый геометрический смысл.
Действительно, рассмотрим уравнение касательной к графику функции 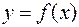 в точке
в точке 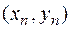
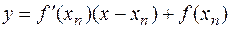
и определим её точку пересечения с осью ох. Имеем  , откуда
, откуда
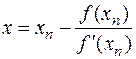 .
.
Из сравнения полученного выражения с (4.2) следует вывод, что
абсцисса точки пересечения касательной, проведённой к графику функции в точке 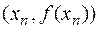 и представляет собой следующее приближение к решению уравнения (4.1) (Рисунок 4.2). и представляет собой следующее приближение к решению уравнения (4.1) (Рисунок 4.2).
|
 |
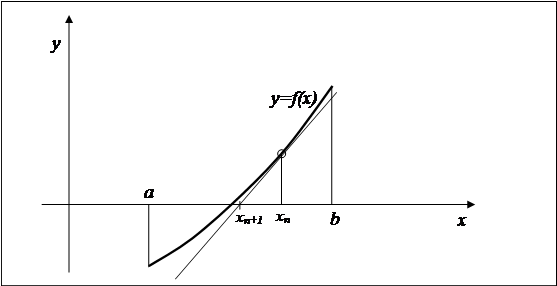
Рисунок 4.2. Метод Ньютона
По этой причине метод Ньютона называют ещё методом касательных.
Метод хорд. Рассмотрим (4.3). Заменим в нём
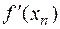 на
на 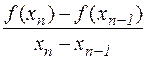 .
.
В результате этого получим новое вычислительное правило
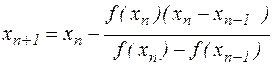
| (4.4) |
называемое методом хорд.
Выясним его геометрический смысл.
Рассмотрим точки кривой 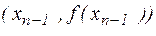 ,
,  и проведем через них прямую
и проведем через них прямую
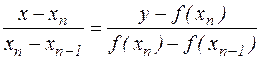 .
.
Найдем, далее, ее точку пересечения с осью абсцисс. Имеем
 ,
, 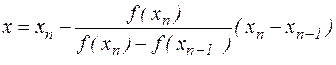 .
.
Сравнивая полученные выражения с соотношением (4.4), приходим к выводу, что
| абсцисса точки пересечения прямой, проходящей через точки кривой, определяемые двумя последними приближениями, представляет собой следующее приближение к решению уравнения (4.1) (Рисунок 4.3). |
 |

Рисунок 4.3. Метод хорд
 Сходимость, оценка погрешности. Рассмотрим эти вопросы на примере метода Ньютона.
Сходимость, оценка погрешности. Рассмотрим эти вопросы на примере метода Ньютона.
Рассмотрим отображение
 ,
,
где 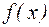 , - левая часть уравнения (4.1),
, - левая часть уравнения (4.1),  .
.
Заметим, что неподвижная точка отображения 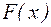 , если она есть, является и решением уравнения (4.1). Действительно, пусть существует значение х такое, что
, если она есть, является и решением уравнения (4.1). Действительно, пусть существует значение х такое, что 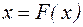 . Отсюда
. Отсюда
 ,
,
откуда 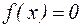 , что и требовалось.
, что и требовалось.
Далее, пусть 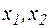 , - произвольные значения х, оценим величину
, - произвольные значения х, оценим величину  . Имеем
. Имеем

Тогда по теореме Лагранжа

где  , или
, или
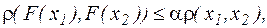
где  .
.
Отсюда следует утверждение.
Если 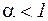 или, что то же или, что то же  , то отображение , то отображение 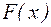 является сжимающим, последовательность (4.3), им формируемая,является сходящейся и, следовательно, метод касательных в этом случае сходится. является сжимающим, последовательность (4.3), им формируемая,является сходящейся и, следовательно, метод касательных в этом случае сходится.
|
Предельная точка х последовательности (4.3) является неподвижной точкой отображения 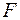 и является искомым решением. Погрешность
и является искомым решением. Погрешность 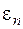 , - n -го приближения к решению, как и ранее, описывается соотношением (3.10).
, - n -го приближения к решению, как и ранее, описывается соотношением (3.10).
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 267; Нарушение авторских прав?; Мы поможем в написании вашей работы!