
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 5. Решение систем нелинейных уравнений
|
|
|
|
Задание
1. Путем ручного просчета найти корень заданного уравнения двумя методами (из четырех рассмотренных) с заданной точностью. Отделение корней провести графически. Привести все необходимые промежуточные вычисления. Результаты свести в итоговую таблицу:
| № итерации | Xn | |Xn-Xn-1| или |Bn-An| | F(Xn) |
Замечание. Для каждого уравнения необходимо найти один корень. Если уравнение имеет более одного корня, необходимо отыскать ближайший к началу координат.
Номер уравнения выбрать по формуле: k+21*(q-1).
Здесь k – номер студента в списке группы; q=1 для группы А и 2 для группы Б.
Допустимая погрешность вычисляется по формуле:
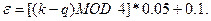
Номера применяемых методов (1-дихотомии; 2-хорд; 3-касательных; 4-простой итерации) вычислить по формуле:
N1=(k-q)MOD 2+1; (первый метод)
N2=[(k+q)DIV 2]MOD 2+3 (второй метод).
Варианты к заданию
1. 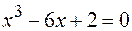 .
.
2.  .
.
3. 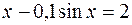 .
.
4. 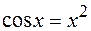 .
.
5. 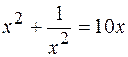 .
.
6. 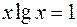 .
.
7. 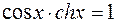 .
.
8. 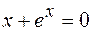 .
.
9. 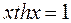 .
.
10.  .
.
11.  .
.
12. 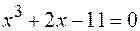 .
.
13. 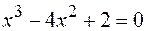 .
.
14. 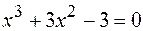 .
.
15. 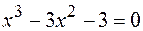 .
.
16. 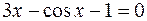 .
.
17. 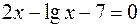 .
.
18. 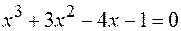 .
.
19. 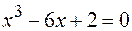 .
.
20.  .
.
21.  .
.
22. 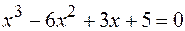 .
.
23. 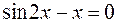 .
.
24. 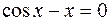 .
.
25. 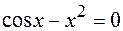 .
.
26. 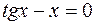 .
.
27.  .
.
28. 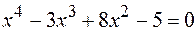 .
.
29.  .
.
30.  .
.
31.  .
.
32. 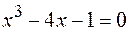 .
.
33. 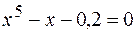 .
.
34.  .
.
35.  .
.
36.  .
.
37. 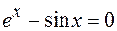 .
.
38.  .
.
39. 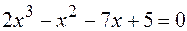 .
.
40.  .
.
41. 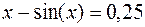
42. 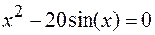
43. 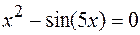
44. 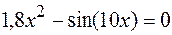
45. 
В которой, рассмотренные выше, методы Ньютона и итераций обобщаются на случай систем нелинейных уравнений.
Ниже ограничимся рассмотрением метода итераций и метода Ньютона, которые относятся к числу основных.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 335; Нарушение авторских прав?; Мы поможем в написании вашей работы!