
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 7. Методы решения обыкновенных дифференциальных уравнений
|
|
|
|
Задание
1. Применяя ручной просчет, вычислить значение заданного определенного интеграла (согласно варианту задания) с точностью 0,005*(1+k MOD 6) одним из 3-х методов:
1) прямоугольников;
2) трапеций;
3) Симпсона.
Метод выбрать по формуле: (k-1)MOD 3+1. k – номер студента в списке группы.
Построить график подынтегральной функции на отрезке интегрирования. Необходимое количество разбиений отрезка интегрирования для каждого из методов найти, используя соответствующие формулы для погрешности. Привести все промежуточные вычисления и построить графики всех необходимых функций.
2. Составить программу, вычисляющую значение данного интеграла тремя указанными методами с произвольно заданной точностью. Контроль точности производить по методу Рунге (двойного просчета):
|IN-I2N|/(2m-1) < e,
где IN и I2N – значения интеграла, найденные с числом подотрезков, равным соответственно N и 2N; m – порядок точности метода.
Входные данные программы: значение допустимой погрешности и начальное количество разбиений отрезка интегрирования (одинаковое для всех методов). Выходные данные: значение интеграла, найденные каждым методом и конечное число подотрезков для каждого метода.
Результаты расчетов свести в итоговую таблицу:
| Методы | |||
| Прямоугольников | трапеций | Симпсона | |
| Значение интеграла | |||
| Кол-во разбиений |
Варианты заданий
1. 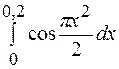
2. 
3. 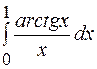
4. 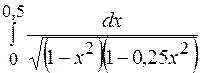
5. 
6. 
7. 
8. 
9. 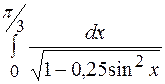
10. 
11. 
12. 
13. 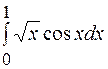
14. 
15. 
16. 
17. 
18. 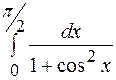
19. 
20. 
21. 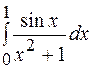
22. 
23. 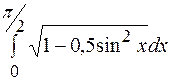
24. 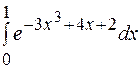
25. 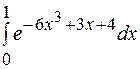
В которой рассматриваются простейшие аналитические последовательных приближений и рядов Тейлора) и численные (Эйлера, трапеций и Рунге-Кутта) методы решения задачи Коши обыкновенных дифференциальных уравнений.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 290; Нарушение авторских прав?; Мы поможем в написании вашей работы!