Численные методы решения. Правило Рунге

Классификация методов. Производится в зависимости от особенностей той информации, которая используется при вычислении приближенного значения y(x) в узловой точке.

В первом приближении правило, по которому происходят вычисления символически можно представить в виде

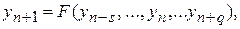(5)

где

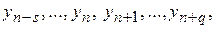- приближенные значения решения задачи (1), (2) в точках

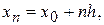
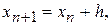
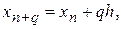
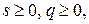
h – шаг интегрирования. Если

1) 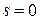, а , то правило (5) называется одношаговым, в противном случае,- многошаговым;

2) 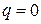, вычислительное правило называется явным, при 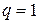неявным, при 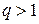, - с забеганием вперед.

Далее, основное внимание уделим одношаговым методам. Соответствующее вычислительное правило имеет вид

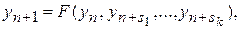
где .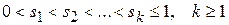

Методы, основанные на разложении в ряд Тейлора. Предположим, что узлы интегрирования являются равноотстоящими, т.е. 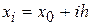и рассмотрим участок 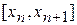. Предполагая функцию 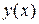дифференцируемую достаточное число раз, имеем

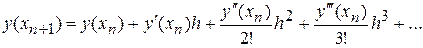(6)

Ограничиваясь малыми первого порядка относительно h, получим правило

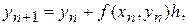(7)

которое называется явным методом Эйлера. Его погрешность на отрезке 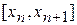составляет

,

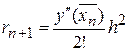где 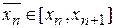, а на конечном отрезке [ a, b ] учитывая 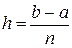, равна

,

где 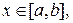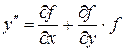. На основании этого данный метод называется методом первого порядка точности. Он имеет наглядную геометрическую интерпретацию (Рисунок 1) и называется также методом ломаных. На каждом участке длиной h участок интегральной кривой заменяется отрезком прямой.

Рисунок 1. Явная схема Эйлера.

Замечание 1. Если воспользоваться разложением

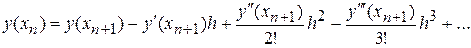(8)

и также ограничиться малыми первого порядка, получим правило

(9)

которое называется неявной схемой Эйлера.

Погрешность формулы (9) равна

,

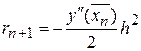погрешность метода на конечном промежутке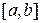

.

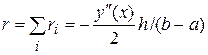Замечание 2. Сложим (7), (9) и разделим на два, в результате чего получим новое правило

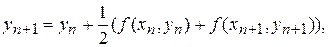называемое методом трапеций. Также как и (9) оно является неявным. Если из разложения (6) почленно вычесть разложение (8), получим локальную погрешность формулы трапеций

.

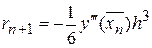Тогда погрешность, накапливаемая на отрезке 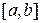будет равна

,

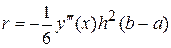где 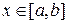. Таким образом, метод трапеций имеет второй порядок точности.

Замечание 3. Рассмотренные выше погрешности приближенных методов описывают те ошибки, которые возникают вследствие замены дифференциального уравнения конечной вычислительной схемой и называется погрешностью аппроксимации. Помимо этого в общем балансе играют роль погрешности, возникающие на каждом шаге интегрирования в результате использования приближенного значения 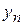вместо точного 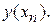Их обычно относят к погрешностям обусловленным неточностями в задании исходных данных и рассматривают отдельно.

Методы Рунге-Кутта. Рассмотрим уравнение (1). Интегрируя его на промежутке 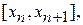получим

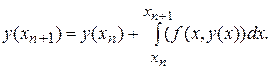
Тогда после замены 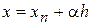, где 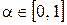, для приращения на n-ом шаге получим выражение

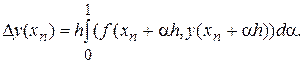(10)

Таким образом, задача вычисления значения функции 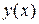в точке 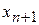сводится к вычислению интеграла в соотношении (10). Однако использование традиционных квадратурных формул для этих целей проблематично, так как значения 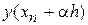неизвестны. В методах Рунге – Кутта квадратурные схемы строятся следующим образом.

Вводятся три группы параметров 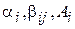, где

,

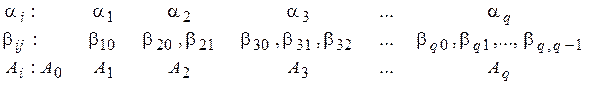которыми распоряжаются так. Первая группа параметров определяет набор узловых значений 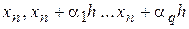по первой переменной подинтегральной функции 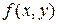. Вторая группа параметров определяет набор узловых значений по ее второй переменной. Причем производится это косвенным образом через приращения 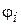функции 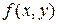в предыдущих узловых точках, где

,

,

,

........

.

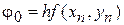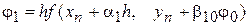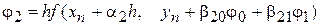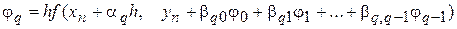Наконец, третья группа параметров 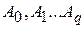используется для формирования квадратурной формулы

.

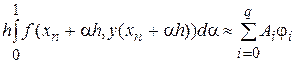Таким образом, окончательно

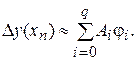(11)

Обозначим погрешность соотношения (11) через 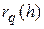, т.е.

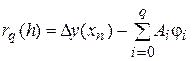
или

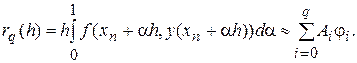
Представим ее с помощью формулы Тейлора в виде разложения по степеням h

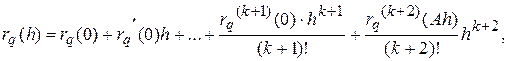
где .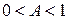

Если потребовать теперь, чтобы 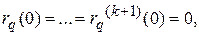получим погрешность соотношения (11) равную 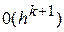и, следовательно, погрешность метода равную .

К числу наиболее употребительных относятся методы 4-го порядка точности. Для них значение 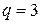. Один из вариантов соответствующего набора параметров следующий

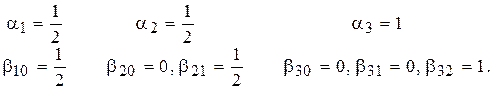
Тогда выражения 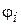имеют вид

,

,

,

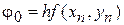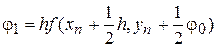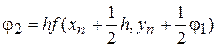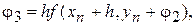
коэффициенты ,-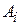

, , ,

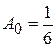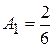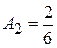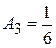
и вычислительное правило, в целом,

.

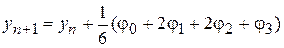На Рисунке 2 в полосе указаны используемые в этом методе узловые точки. Значения 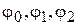выбраны произвольно.

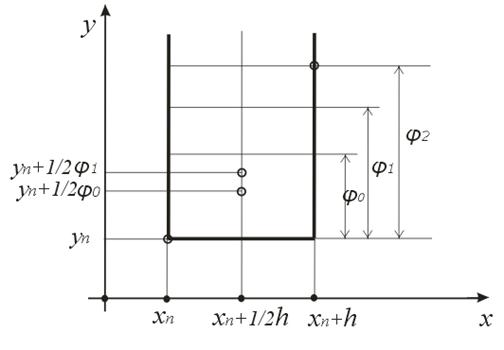
Рисунок 2. Узловые точки метода Рунге-Кутта 4-го порядка

Правило Рунге. Для оценки погрешности численных результатов интегрирования при использовании одношаговых методов на практике обычно применяют правило Рунге, которое заключается в следующем.

Теоретически показано, что главный член погрешности аппроксимации имеет вид 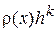, где k – порядок метода, 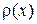- некоторая функция, определяемая особенностями правой части дифференциального уравнения.

,

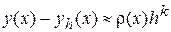где 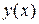, - точное значение, 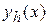, приближенное, определенное при проведении расчетов с шагом h. Тогда, проводя расчеты с шагом 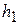и 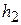, получаем

.

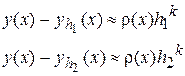Разрешая, далее, приближенную систему этих соотношений относительно 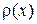, имеем

,

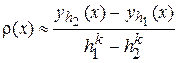откуда

. (12)

Соотношение (12) и представляет правило Рунге. Естественно, оно дает достоверные результаты лишь в том случае, когда доминирующей в общей погрешности результата является погрешность метода.

Обычно правило (12) используют при 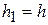, 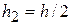. Тогда

.

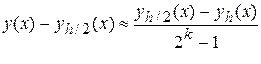В частности, для методов Эйлера (k=1)

,

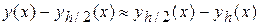метода трапеций (k =2), -

,

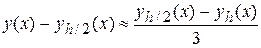метода Рунге – Кутта четвертого порядка (k =4),-

.

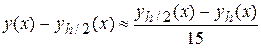Дата добавления: 2014-01-06