Элементы общей теории

Задание

1. Найти методом Пикара три первых приближения решения заданной (согласно варианту задания) задачи Коши для обыкновенного дифференциального уравнения первого порядка. Привести все необходимые расчеты. Построить графики соответствующих функций.

2. Для той же задачи Коши при помощи ручного просчета найти интегральную кривую методом Рунге-Кутта 4-го порядка на отрезке единичной длины (начиная от X₀) с шагом 0,2. Привести все промежуточные расчеты. Окончательные результаты расчета свести в таблицу. По результатам построить график.

3. Построить Simulink-модель для заданной задачи Коши по условиям предыдущего пункта. Сравнить результат (представленный в виде графика) с результатом п.2.

Варианты заданий

1.

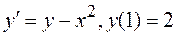
2.

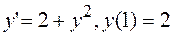
3.

4.

5.

6.

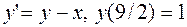
7.

8.

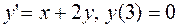
9.

10.

11.

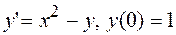
12.

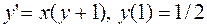
13.

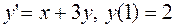
14.

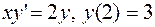
15.

16.

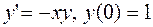
17.

18.

19.

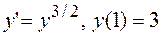
20.

21.

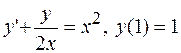
22.

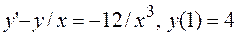
23.

24.

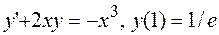
25.

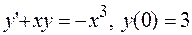
Лекция 8. Основы спектрального анализа

В которой напоминаются основные положения теории рядов Фурье, производится вывод комплексной формы и приводится их дискретный аналог для равноотстоящих узлов.

Напомним основные положения теории рядов Фурье.

Пусть имеется некоторая функция , заданная на промежутке 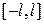и рассматривается бесконечная система функций

.

Ставится задача о представлении данной функции в виде тригонометрического ряда

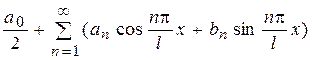(1)

Такое представление при определенных условиях возможно и его коэффициенты вычисляются по следующим формулам

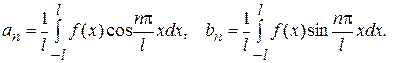(2)

Тригонометрический ряд (1) с коэффициентами (2) называется рядом Фурье функции .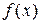

Справедлива следующая теорема о разложимости (т. Дирихле):

Если 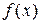кусочно-монотонная функция и имеет не более, чем конечное число точек разрыва первого рода, то ее ряд Фурье (1), (2) сходится к значению 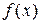в точках ее непрерывности и к среднему арифметическому ее односторонних пределов в точках разрыва.

Так, например, если 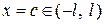точка разрыва 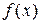, то сумма ряда Фурье в этой точке равна

- (Рисунок 1),

где

, .

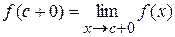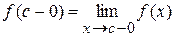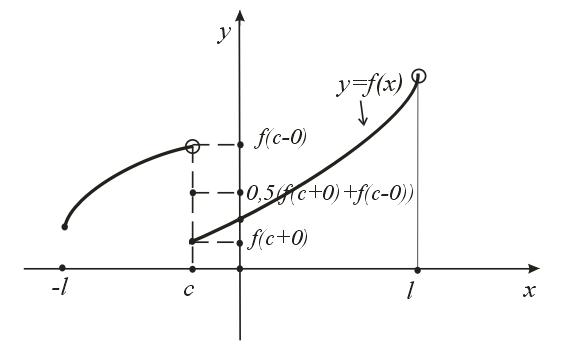
Рисунок 1. Пояснения к теореме Дирихле

Т.о. за исключением, быть может, конечного числа точек сумма ряда Фурье (1), (2) равна .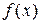

Замечание 1. В точках ряд Фурье сходится к среднему арифметическому правого и левого пределов функции 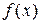в точках 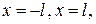соответственно.

Обратим внимание на особенности разложения в ряд Фурье четных и нечетных функций.

Если 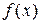четная на отрезке 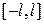, то 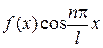, также четная, а 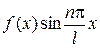, - нечетная. Поэтому коэффициенты

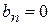
и разложение (1) принимает вид

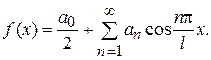
Если же функция 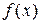нечетная, то 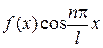также нечетная, а 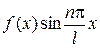, - четная.

Поэтому

,

и разложение (1) принимает вид

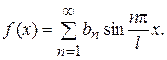
Замечание 2. Выражение 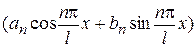в разложении (1), вводя вспомогательный угол, можно представить в виде , где и ряд в целом

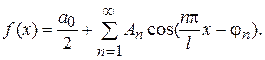
Тогда слагаемые называются гармоническими составляющими или гармониками, коэффициенты 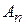- амплитудами гармоник, частотами, - начальными фазами. Иногда гармоника называется основной, гармоники 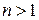, - побочными.

Замечание 3. Иногда тригонометрические разложения заданной функции строятся на промежутке 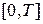. В этом случае рассматривается система тригонометрических функций

1, ,

и разложение имеет вид

(3)

где

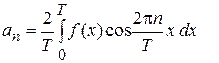(4)

.

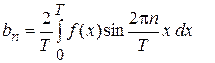Теорема Дирихле для промежутка формулируется соответственно аналогичным образом.

Дата добавления: 2014-01-06